Factorial Design, the Right Way

When two or more factors, each in two or more levels, are to be tested for their combined effect on the quality characteristic—the dependent variable—-factorial design is appropriate. The follow­ing is an example of three factors at two levels.

Example 7.2

In a sheet metal press, it is the intention to measure the quantity of deformation of a metal sheet with various combinations of three factors: press pressure (p), duration of press action (d), and temperature of plate (t). If each factor is to be tried at two levels, (Pi,p2), (dj, df), and (tj, tf), we have the following eight treat­ments with different settings of factors:

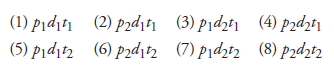
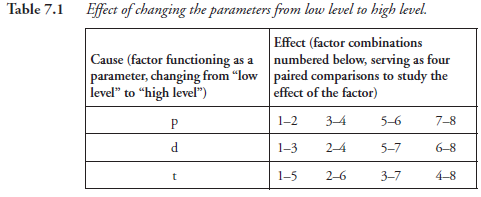
Comparing (1) and (2) above, we notice that d^ is common between the two, and there is change in p alone; p functions as an independent variable (cause) with consequent change in the dependent variable (effect) observed or measured and recorded. Combination pairs (3)-(4), (5)-(6), and (7)-(8) also show p in the role of independent variable, with other factors remaining same. Together, we have four cases in which the effect of chang­ing the parameter, p (the cause), from level p₁ to p₂ can be observed. Each of these is analogous to the paired comparison tests we discussed earlier; instead of the factors being present or absent completely, we now have the factor functioning at two levels, p1 and p2.

Similar cases can be made for the parameters d and t also; the summary is shown in Table 7.1.

Instead of the above scheme, which is the essence of factorial design, if we resorted to a one-factor-at-a-time schedule to obtain, as above, four comparisons of each of the three factors, each at two levels, we would require 4 x 3 x 2 = 24 treatments, and that too, not as appropriately as the eight treatments dis­cussed above.

Source: Srinagesh K (2005), The Principles of Experimental Research, Butterworth-Heinemann; 1st edition.