The Intrinsic Geometry of Phenomena

I.Kohler (1953) claims that the word “space” has different denotations depend­ing on its use in physics, mathematics or psychology. Nevertheless he contends that the geometry of space might be envisaged even in the psychology of per­ception, provided the epistemological difference between these denotations is taken into account. In mathematical geometry the definition of concepts like “straight,” “length,” “line” and so on does not require reference to the percep­tion of the corresponding property or entity. The only exception, perhaps, is the concept of “coincidence” without which any measure would not be pos­sible (see Schlick, 1918). To be sure, in physics the definition of a geometrical concept also has to coordinate it with the particular physical object to which it applies, rather than solely defining its meaning by reducing it to other con­cepts. For this reason Reichenbach (1928: 23) has introduced the notion of “co- ordinative definition.” The concepts of geometry can be coordinated with the objects of any physical domain if these objects have the same role in their do­main that geometrical concepts have in order to satisfy the abstract relational structure of geometry. Therefore the definition is not arbitrary, notwithstand­ing the arbitrariness of the elementary concepts of geometry.

Kohler remarks that we don’t have the same freedom in choosing what the perceptual instance of a point, a straight line or the equality of length and angles would be. Nonetheless, this does preclude a geometry of perception, if it is intended as the analysis of properties of perceptual space as they appear in the restricted domain of perception, rather than as the application of the con­cepts of geometry to the latter to see whether or not they are consistent with the physical space (1953: 226). Besides, it is reasonable that perceptual space has its own systematic regularity, because it is conceivable that geometry could not have been constructed without the clue (Anlafi) of spatial perception just as was the case with the theory of heat and the percetion of temperature. In­deed, the fact that railway tracks appear to deviate from parallelism and the sky vault appears flattened instead of as a hemisphere implies that subjects are able to determine how visual things should look were they to satisfy such geometrical properties.

Therefore, the geometry of perception should reject a construct like that of “sensory illusion,” because its validity presupposes that a coordinative defi­nition has been established between entities of distinct domains. The geom­etry of perception does not deal with the correspondence of phenomena with the geometry of the stimulation. It is by definition restricted to phenomena; hence, what counts as a rigid body must not be derived from other domains. Rather, one has to look for what preserves equal perceived distance across dif­ferent places in the perceptual domain itself (1953: 227). Kohler claims it is al­ways possible to determine the mechanical deformations that make a physical object look as if it has the same size at different distances as well as the same length at different places. In accord with a fundamental claim of phenomenol­ogy, however, he maintains that the perceptual measurement unit for what is perceptually straight can be constructed on the grounds of what appears straight, rather than bent or wavy, by employing stimuli as auxiliary means to bring about the desired perceptual units with the most accuracy and constan­cy as possible. The observation that equal physical distances happen to not coincide with perceptually equal distances implies only that the geometry of perception needs a more complicated measurement unit of congruence than physical geometry. As Gauss tried to prove the validity of Euclidean geometry in the physical world by measuring the distance between material things, the peaks of three mountains, through the physical means of light, so perceptual points, straight lines and distance equality have to be the only means to prove whether defined spatial relations hold among them in the perceptual domain. Kohler then contends that the geometry of perception can employ a method of phenomenal construction. The first step would be to investigate the conditions in which a visual line connects two points so that it is impossible to lay down another line between them that is similar to and distinguished from it (see Rubin’s work discussed below). This would be the definition of a perceptual straight line. The next step would be to mark out the perceived equal distances on such straight lines. Subjects would be asked to join such perceptual units to­gether to build a triangle with sides that are straight and of equal length. Then, questions on the perceived magnitude of angles and their relations with sides would be addressed. If it were found that in particular conditions subjects can­not see the relation that would be expected on the grounds of Euclidean geom­etry, this would count as a paradox in Rubin’s sense.

1. The Elements of the Geometry of Phenomena

Rubin (1922) shows how some fundamental entities of the geometry of percep­tion can be defined from perceptual experience. He notes a difference with Buhler (1913: 7if.), who also studied the conditions at which a given physical line appears straight or curved. Buhler used as stimuli the arcs of a circle and physically straight lines in the frontal-parallel plane. Every stimulus is defined by the position in the plane, the height or the distance from the middle point of the arc to the chord, the chord length. Keeping the chord constant while increasing or decreasing the height, by making the radius of the circle longer or shorter, Buhler derived the height thresholds: a for perceiving a curved line on the right of the middle point and b for perceiving a curved line on its left. The threshold for the appearance of a straight line is then measured by a + b/2. Buhler found that appearances of physically straight lines fluctuate, although within a narrow range. Thus he claimed that since physical lines cannot but be constant, it is reasonable to assume that the subjects use these varying appear­ances to judge whether or not the line is actually straight. Rubin remarks that Buhler reasons as if appearances were only the varying aspects of a constant material or physical object. In such a case, the research assumes that material objects have constant properties that yet are differently shown in the correlat­ed appearances, which are accordingly studied only under the respect of their adequacy to constant non-perceptual properties. Instead, Rubin emphasizes that the research has to deal with perceptual appearances just as they are. In this sense the spatial features of appearances are no longer the varying aspects of spatial properties of physical objects, but rather many instances of the forms of phenomenal space. Thus an autonomous geometry of perception can be constructed on the grounds of the evidence of what is a perceptual straight line and whether or not only one line can be perceived to pass between any two vi­sual points. Rubin measures the thresholds for the appearance of a straight line and the visual discrimination of two lines, whose average values in visual an­gles are respectively 11″ and 30″. He then presents two lines between two points, which physically can either be one straight and one curved, or both curved. Their greatest distance can be equal to a + b. To see two separate lines this sum must be greater than 30″, while to see two straight lines this sum must not be greater than 22″. Therefore, it is impossible that there could be the appearances of two distinct straight lines passing both between the same two points.

To prove the independence of such a geometry of perception Rubin shows that some fundamental definitions of geometry do not hold for appearances, for instance the definition of a straight line as the shortest path between two points.^[1] He extends this claim to the geometric definitions of order. Rubin makes reference to Pasch, whose axioms can in fact be applied in many cases even to visual entities. Indeed, Pasch (1926) contends that the fundamental concepts of geometrical shape, size and mutual positions are introduced by pointing out appropriate natural objects. He maintains that even axioms are in reality grasped in the corresponding geometrical figures, unlike theorems whose proof is freed from reference to any perceptual content (1926: 16, 43). However, Rubin remarks that the axioms of continuity and order may not cap­ture the form of order that the figures display from the perceptual standpoint. For example, in figures such as lines composed of points, the order may de­pend on the belongingness of parts rather than on the property of being be­tween one another. According to one of Pasch’s axioms of order: (i) between two points a and c there is always a third point; (ii) if b lies between a and c, and if c lies between b and d, then b lies between a and c. In figure 33 the axiom is perceptually satisfied by the dots lying along a straight line on the right.

Yet it is sufficient to change the distance between points while preserving the arrangement to let two perceptual orders emerge on the left and the right, which hence are beyond the scope of the axiom. On the left, b and c now ap­pear to belong to each other. They form a visual unity so that b is not perceived as lying between a and c. Rather it is the pair (b, c) that appears to be between a and d. On the right, the perceptual order corresponds to two pairs (a, b) and (c, d). Neither b nor c is perceived as an independent point lying between the others.

Moreover, Rubin remarks that perceptual belongingness is not transitive. In figure 34, a and b as well as b and c are perceived to belong to each other, but this does not hold for a and c, because they appear to be connected to b within two distinct visual lines.

Although Rubin does not mention it, it is noteworthy that such a perception is possible because b plays two different phenomenal roles at once that require it to enter two different relations of order.

Rubin puts forth the example in the figure 35 to show that structural fea­tures, which bind together the visual elements into a connected unit, may be so strong that they compete against the observation of sub-units that would satisfy some geometrical relations.

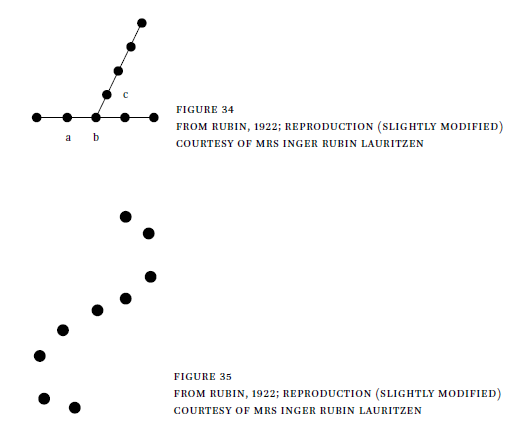
In such cases, Rubin suggests that a grouping factor enables one to see the points arranged and ordered as parts of a curved figure, so that it is difficult to see that in several parts of it there are points lying on a straight line.

Source: Calì Carmelo (2017), Phenomenology of Perception: Theories and Experimental Evidence, Brill.