Applications of Randomization

Obtaining samples or specimens from a group (also known as a lot or population) of any kind is an activity wherein the applica­tion of randomness is of utmost significance. In the case of the study by pairing, a toss of the coin serves the purpose. Random­ization has applications beyond sampling, for example, in the sequencing of experiments. We will discuss only two obvious sit­uations. Let us say that there is a hypothesis on hand that the per­formance of a certain machine is influenced by the temperature of the room. The experimenter wants to test the performance at 50°F, 60°F, 70°F, 80°F, and 90°F, and there should be five repli­cations at each temperature. The usual “commonsense” approach is to set the room temperature at 50°F and to test the perfor­mance five different times with adequate time gaps between con­secutive tests, then to raise the temperature setting to 60°F, repeat the five tests, and so on, until all twenty-five tests are completed in as many days as required. In this scheme, there is no thought given to randomization. When it is given serious consideration and some randomization is imposed, the scheme of experiment is somewhat like that shown in Table 16.1.

From the results—let us say, various readings and calculation for “performance”—of experiments per this scheme, obviously the performance at 70°F is “averaged” based on the five perfor­mances at that temperature obtained on different days, at differ­ent time periods. But how were the sequences arranged for each day? In the above table, they were “predetermined.” To adhere to the idea of randomization, that ought to be avoided. For instance, the experimenter can use five sheets of paper with one of five temperatures (50, 60, 70, 80, 90) on each sheet, then fold the sheets to make the numbers invisible. At the beginning of each day’s experiment, he has one of the five folded sheets picked by a colleague who is not involved with the experiment. What­ever temperature is found on the sheet is the temperature at which the first performance test of the day is to be conducted. He then has another folded sheet picked out of the remaining four, the temperature written on that sheet being the second test tem­perature in sequence for the day. Then, the third and the fourth are picked, leaving the last, the fifth. This random selection determines the time sequence of the experiments for the day. The experimenter does this sequencing process each day, thereby implementing randomization.

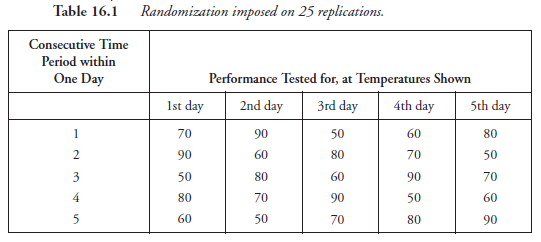
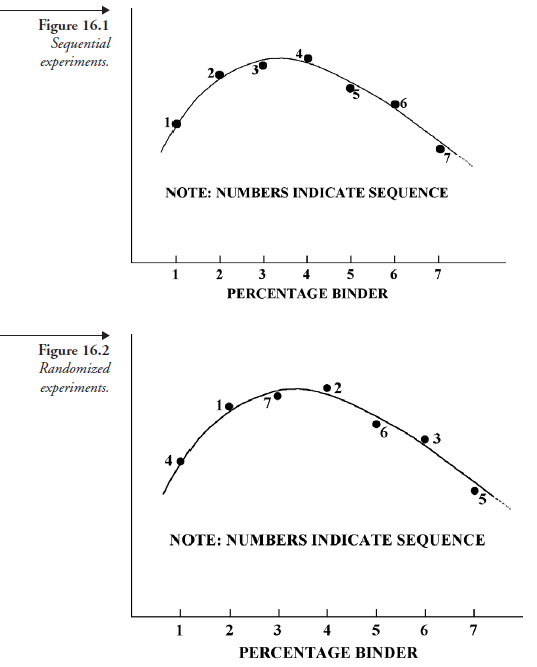
Another situation where randomization is usually ignored, but can be implemented, follows: Suppose an experimenter’s interest is to test a new synthetic sand binder on the market. He wants to mix 1, 2, 3, 4, 5, 6, and 7 percent by weight of the binder with a standardized sample of sand and test it for strength per standard procedure. Let us say he prepared a plot of strength versus percentage of the binder added; it looks like Figure 16.1.

The numbers next to the curve show the time sequence in which the individual tests were performed. Obviously, in this experiment there is no thought of randomization. If, instead, randomization was imposed somewhat on the same basis as we discussed in the previous case, the sequence could be different, as shown in Figure 16.2.

Obviously, there are several such sequences possible, this one arbitrarily “fixed” to be random. In this example, again, the ques­tion may be asked, Though the order 4, 1, 7, 2, 6, 3, 5 does not follow any conceivable mathematical series, is not the very pro­cess of predetermining (or fixing) the sequence against the idea of randomization? Since the answer is yes, this defect can be reme-died as we described previously, by picking numbered sheets that are folded so the numbers are hidden. In this case, each paper would have one number of 1, 2, 3, 4, 5, 6, or 7 (percentages of binder), with the sequence in which they were picked deciding the corresponding sequence for the experiments.

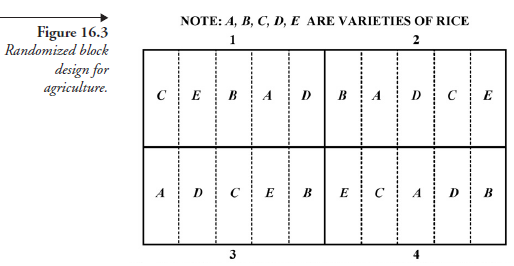
Randomization of land plots for experiments in agriculture, often referred to as two-dimensional spatial design or block design, is one of the earliest applications, pioneered by R. A. Fisher (1890—1962). Suppose five varieties of a farm crop, say rice, are to be tested for productivity or yield in an apparently similar set of conditions: soil, climate, and agricultural treatment. The total experimental area is not simply divided into five parts, and each variety of crop assigned to one part. Instead, the following arrangement, one of many possibilities, is acceptable. The experi­mental area is divided into four rectangular “blocks” about equal in size. Each block, in turn, is divided into five “plots” running from end to end of the block, lying side by side, making, in all, twenty plots. In each of the four blocks, the five plots are assigned one to each variety of the crop under the test; this last assignment is done “at random.” The method for randomization can be pick­ing the papers with hidden numbers, matching any one of 1, 2, 3, 4, or 5 plots with any one of, say, A, B, C, D, or E varieties of crop, or by any other methods available. One of the many possi­bilities of such randomization is shown in Figure 16.3.

Passing over many more contexts and methods of randomiza­tion, we may conclude this list with the case of opinion polls, all too frequently used by the media and eagerly accepted by the public. Seldom do we hear how many people contributed to the opinion, through what means of communication, and using what criteria and method for sampling. Needless to say, if the “poll” is “national,” it should represent all kinds of varieties in the

nation: city, town, and rural; upper, middle, and lower class; learned, educated, and uneducated; men, women, and children; professional, wage earning, and welfare class; old, mature, and young; and so on. Above all these, the important criterion is ran­domization. How it was implemented, we hardly get to know.

Source: Srinagesh K (2005), The Principles of Experimental Research, Butterworth-Heinemann; 1st edition.