Correlation and Regression with SPSS – Problem 8.6: Multiple Regression

The purpose of multiple regression is similar to bivariate regression, but with more predictor variables. Multiple regression attempts to predict a normal (i.e., scale) dependent variable from a combination of several normally distributed and/or dichotomous independent/predictor variables. In this problem, we will see if math achievement can be predicted well from a combination of several of our other variables, gender, grades in high school, and mother’s and father’s education. There are many different methods provided to analyze data with multiple regression. We will use one where we assume that all four of the predictor variables are important and that we want to see what is the highest possible multiple correlation of these variables with the dependent variable. For this purpose, we will use the method the program calls Enter (usually called simultaneous regression), which tells the computer to consider all the variables at the
same time. Our IBM SPSS for Intermediate Statistics book (Leech, Barrett, & Morgan, 4^th ed., in press) provides more examples and discussion of multiple regression assumptions, methods, and interpretation.

Assumptions and Conditions of Multiple Regression

There are many assumptions to consider, but we will only focus on the major ones that are easily tested. These include the following: the relationship between each of the predictor variables and the dependent variable is linear, the errors are normally distributed, and the variance of the residuals (difference between actual and predicted scores) is constant. A condition that can be problematic is multicollinearity; it occurs when there are high intercorrelations among some set of the predictor variables. In other words, multicollinearity happens when two or more predictors are measuring overlapping or similar information.

• How well can you predict math achievement from a combination of four variables: grades in high school, father’s and mother’s education, and gender?

In this problem, the computer will enter or consider all the variables at the same time. We will ask which of these four predictors contribute significantly to the multiple correlation/regression when all are used together to predict math achievement.

Let’s compute the regression for these variables. To do this, follow these steps:

• Click on the following: Analyze → Regression → Linear.... The Linear Regression window (Fig. 8.11) should appear.
• Select math achievement and click it over to the Dependent box (dependent variable).
• Next select the variables grades in h.s., father’s education, mother’s education, and gender and click them over to the Independent(s) box (independent variables).
• Under Method, be sure that Enter is selected.
• Click on Statistics at the top right corner of Fig 8.11 to get Fig. 8.12.
• Click on Estimates (under Regression coefficients), click on Model fit, and Descriptives.

(See Fig. 8.12.)

• Click on Continue.
• Click on OK.

Compare your output and syntax to Output 8.6.

Output 8.6: Multiple Regression

REGRESSION

/DESCRIPTIVES MEAN STDDEV CORR SIG N

/MISSING LISTWISE

/STATISTICS COEFF OUTS R ANOVA

/CRITERIA=PIN(.05) POUT(.10)

/NOORIGIN

/DEPENDENT mathach

/METHOD=ENTER grades faed maed gender.

Regression

Interpretation of Output 8.6

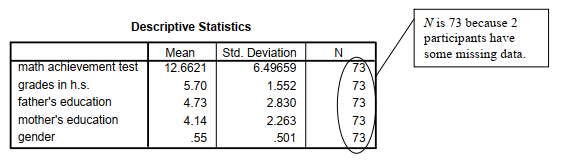
This output begins with the usual Descriptive Statistics for all five variables in the first table. Note that the N is 73 because two participants are missing a score on one or more variables. Multiple regression uses only the participants who have complete data (listwise exclusion) for all the variables. The next table is a Correlation matrix. The first column shows the correlations of the other variables with math achievement. Note that all of the independent/predictor variables are significantly correlated with math achievement. Also notice that two of the predictor/ independent variables are highly correlated with each other; mother’s and father’s education are correlated .68, which is not desirable. It might have been better to use only mother’s (or father’s) education or a combined parents’ education.

The Model Summary table shows that the multiple correlation coefficient (R), using all the predictors simultaneously, is .62 and the Adjusted R² is .34, meaning that 34% of the variance in math achievement can be predicted from the combination of father’s education, mother’s education, grades in h.s., and gender. Note that the adjusted R² is lower than the unadjusted R² (.38). This is, in part, related to the number of variables in the equation. As you will see from the coefficients table, only grades in h.s. and gender are significant, but the other variables add a little to the prediction of math achievement. Because several independent variables were used, a reduction of the number of variables might help us find an equation that explains more of the variance in the dependent variable, once the correction is made. It is helpful to use the concept of parsimony with multiple regression and use the smallest number of predictors needed. The ANOVA table shows that F = 10.40 and is statistically significant. This indicates that the predictors significantly combine together to predict math achievement.

One of the most important tables is the Coefficients table. It shows the standardized beta coefficients, which are interpreted much like correlation coefficients. The t value and the Sig. opposite each independent variable indicates whether that variable is significantly contributing to the equation for predicting math achievement. Thus, grades and gender, in this example, are the only variables that are significantly adding to the prediction when the other three variables are already considered. It is important to note that all the variables are being considered together when these values are computed. Therefore, if you delete one of the predictors, even if it is not significant, it can affect the levels of significance for other predictors. For example, if we deleted father’s education, it is quite possible that mother’s education would be a significant predictor. The fact that both father’s education and mother’s education are correlated with math achievement and with each other makes this possibility more likely.

How to Write About Output 8.6

Results

Simultaneous multiple regression was conducted to investigate the best predictors of math achievement test scores. The means, standard deviations, and intercorrelations can be found in Table 8.2a. The combination of variables to predict math achievement from grades in high school, father’s education, mother’s education, and gender was statistically significant, F(4, 68) = 10.40, p < .001. The beta coefficients are presented in Table 8.2b. Note that high grades and male gender significantly predict math achievement when all four variables are included. The adjusted R² value was .343. This indicates that 34% of the variance in math achievement was explained by the model. According to Cohen (1988), this is a large effect.

Source: Morgan George A, Leech Nancy L., Gloeckner Gene W., Barrett Karen C.

(2012), IBM SPSS for Introductory Statistics: Use and Interpretation, Routledge; 5th edition; download Datasets and Materials.