Intercoder Reliability in Content Analysis

An important measure forjudging the quality of a content analysis is the extent to which the results can be reproduced. Known as intercoder reliability, this measure indicates how well two or more coders reached the same judgments in coding the data. Among the variety of methods that have been proposed for estimating intercoder reliability, we discuss three.

A simple and commonly used indicator of intercoder reliability is the observed agreement rate. The formula for this is

where

P₀ = observed agreement rate,

n_a = number of agreements, and

n₀ = number of observations.

Table III.l gives an example from Krippendorff (1980). Coders A and B have each assigned category labels 0 or 1 to a total of 10 recording units. They agree in 6 out of 10 cases, so

Although this indicator is simple, the observed agreement rate is not acceptable because it does not account for the possibility of chance agreement. This is important because even if two coders assign codes at random, they are likely to agree at least to some extent. The expected agreement rate arising from chance can be calculated and used to make a better estimate of intercoder agreement.

The chance agreement rate is fairly easy to compute when the data are redisplayed as in table III.2. Each pair of observations from coders A and B will fall into one of four cells: (1) A and B agree that the code is 0, (2) A codes 0 and B codes 1, (3) A codes 1 and B codes 0, and (4) A and B agree that the code is 1. If we count the number of instances of each pair, the results can be displayed as in table III.2.

The following formula gives the chance agreement rate:

where

Pc = chance agreement rate,

n_i = observed row marginals (from table III.2),

n._i= observed column marginals (from table III.2), and

n= number of observations.

Using the numbers in table III.2, the chance agreement rate is

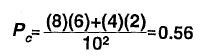
Now the observed agreement rate of 0.6 does not look so good because, by chance, we could have expected an agreement rate of 0.56.

The chance agreement rate is accounted for in a widely used estimate of intercoder reliability called Cohen’s kappa (Orwin, 1994). The formula is

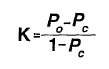
where

K= kappa,

Po = observed agreement rate, and

P_c= chance agreement rate.

With the data in table III.2, kappa is

Kappa equals 1 when the coders are in perfect agreement and equals 0 when there is no agreement other than what would be expected by chance. In this example, kappa shows that the extent of agreement is not very large, only 9 percent above what would be expected by chance.

Kappa is a good measure for nominal-level variables, and it is computed by standard statistical packages such as SPSS. Seigel and Castellan (1988) discuss kappa, including a large-sample statistic for significance testing. Kappa can be improved upon Appendix III Intercoder Reliability

when the variables are ordinal, interval, or ratio. Krippendorff (1990) provides very general, but more complicated, measures. Software programs for computing such variables have been developed in some design and methodology groups within GAO.

Source: GAO (2013), Content Analysis: A Methodology for Structuring and Analyzing Written Material: PEMD-10.3.1, BiblioGov.