Paralleling the situation when you might want to meta-analyze means and standard deviations—that is, when included studies share a common (or comparable) scale for variable X—there may also be instances when we are interested in comparing two groups on a variable measured on a common scale across studies. For example, studies may all compare two groups on variable X using a common scale for X. Although Chapter 5 described the value of standardizing mean differences (e.g., g), in this situation of common scales across studies, it may be more meaningful to meta-analytically combine and compare studies on this common scale. In other words, it may sometimes be useful to retain the meaningful metric of the scale on which variables were measured in primary studies (see also Becker, 2003).
There are various circumstances in which you may prefer to compare two groups in terms of raw rather than standardized differences. For example, gender differences in height may be more meaningful when expressed as inches than as number of standard deviations. Similarly, the effectiveness of a weight-loss program might be more meaningful if expressed in pounds (e.g., the treatment group lost, on average, 10 pounds more than the control group). If you are meta-analytically combining or comparing studies that all use the same measure of the variable of interest (or at least measures that use the same scale), it is straightforward to use these raw, or unstandardized, differences as effect sizes.
The unstandardized mean is simply the raw difference in means between two groups (Lipsey & Wilson, 2001, p. 47):
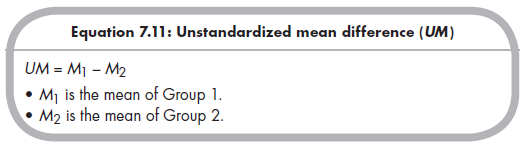
You probably recognize this equation from Chapter 5, where we discussed the various standardized mean differences (Equations 5.5 to 5.7). In Equation 7.11, however, there is no denominator involving some variant of the standard deviation. This standard deviation denominator of Equations 5.5 to 5.7 served to standardize the mean differences in terms of standard deviation units. Here, where the metric is meaningful, you do not wish to standardize this mean difference, but instead leave it in its unstandardized, or raw score, metric.
To estimate the standard error of this unstandardized mean difference (for weighting in your meta-analysis; see Chapter 8), you use the following equation (see Bond, Wiitala, & Richard, 2003; Lipsey & Wilson, 2001, p. 47):

Once you have computed unstandardized mean differences and associated standard errors for each study, it is then possible to meta-analytically combine and contrast these metrically meaningful effect sizes. However, Bond and colleagues (2003) discourage reliance on these traditional techniques and suggest more complicated procedures.6 I suspect that their cautions are most appropriate when studies have small sample sizes and that the increase in precision from their more advanced techniques diminishes with larger sample sizes. However, further quantitative studies are needed to evaluate this claim. Regardless, their alternative formulas do not affect the computation of a mean effect size, but rather inferences about this effect size and heterogeneity. For now, I encourage you to consider the alternative formulas of Bond et al. (2003) if you are meta-analyzing unstandardized mean differences from studies with small sample sizes and your initial analyses of significance of the mean effect or test of heterogeneity are very close to your chosen level of statistical significance. In other cases, you may find the standard methods described in Chapter 8 more straightforward with little substantive impact on your results.
Source: Card Noel A. (2015), Applied Meta-Analysis for Social Science Research, The Guilford Press; Annotated edition.

25 Aug 2021
25 Aug 2021
25 Aug 2021
24 Aug 2021
24 Aug 2021
24 Aug 2021