Maximum-Likelihood Factoring by using Stata

Maximum-likelihood factoring, unlike Stata’s other factor options, provides formal hypothesis tests that help in determining the appropriate number of factors. To obtain a single maximum- likelihood factor for the planetary data, type

The ml output includes two likelihood-ratio % ² tests:

LR test: independent vs. saturated

This tests whether a no-factor (independent) model fits the observed correlation matrix significantly worse than a saturated or perfect-fit model. A low probability (here 0.0000, meaningp < .00005) indicates that a no-factor model is too simple.

LR test: 1 factor vs. saturated

This tests whether the current 1-factor model fits significantly worse than a saturated model. The low p-value here suggests that one factor is too simple, as well.

Perhaps a 2-factor model will do better:

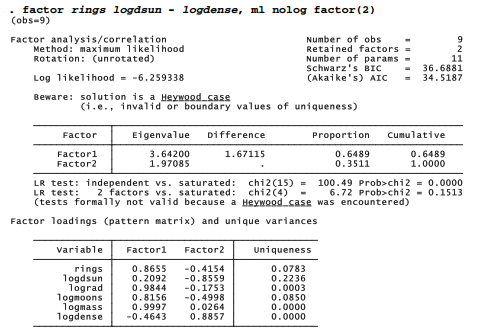
Now we find the following:

LR test: independent vs. saturated

The first test is unchanged; a no-factor model is too simple.

LR test: 2 factors vs. saturated

The 2-factor model is not significantly worse (p = .1513) than a perfect-fit model. These tests suggest that two factors provide an adequate model.

Computational routines performing maximum-likelihood factor analysis often yield Heywood solutions, or unrealistic results such as negative variance or zero uniqueness. When this happens (as in the 2-factor ml example above), the %² tests lack formal justification. Viewed descriptively, the tests can still provide informal guidance regarding the appropriate number of factors.

Source: Hamilton Lawrence C. (2012), Statistics with STATA: Version 12, Cengage Learning; 8th edition.