The examples above involve principal component factoring, specified by the command factor with option pcf. Other factor options perform different kinds of factor analysis.
pcf Principal component factoring
pf Principal factoring (default)
ipf Principal factoring with iterated communalities
ml Maximum-likelihood factoring
Principal factoring extracts principal components from a modified correlation matrix, in which the main diagonal consists of communality estimates instead of 1’s. The factor options pf and ipf both perform principal factoring. They differ in how communalities are estimated:
pf Communality estimates equal R2 from regressing each variable on all the others.
ipf Iterative estimation of communalities.
Whereas principal component analysis focuses on explaining the variables’ variance, principal factoring explains intervariable correlations.
We apply principal factoring with iterated communalities (ipf) to the planetary data:
. factor rings logdsun – logdense, ipf
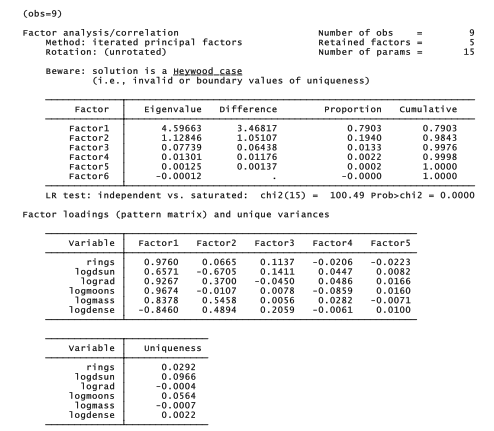
In this example, Stata gives an ominous warning: “Beware: solution is a Heywood case.” Clicking on the linked Heywood case warning yields an explanation of the problem which, in this instance, reflects our unusually small sample (n = 9). For simplicity, we will continue the analysis anyway, but in research such a warning should caution us to rethink our approach.
Only the first two factors have eigenvalues above 1. With pcf or pf factoring, we can simply disregard minor factors. Using ipf, however, we must decide how many factors to retain, and then repeat the analysis asking for exactly that many factors. Here we will retain two factors:
. factor rings logdsun – logdense, ipf factor(2)
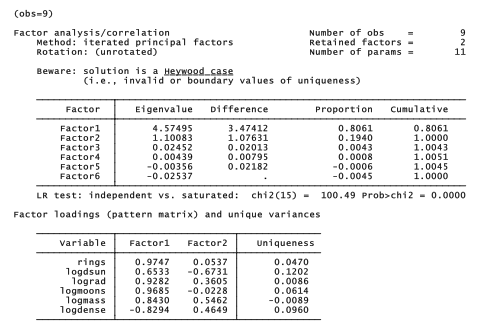
After ipf factor analysis, we could create composite variables using rotate and predict as before. Due to the Heywood-case problem, ipf factor scores here are less plausible than our earlier pcf results. As a research strategy, it often helps to repeat factor analyses using several different methods, and compare these looking for stable conclusions.
Source: Hamilton Lawrence C. (2012), Statistics with STATA: Version 12, Cengage Learning; 8th edition.

23 Sep 2022
28 Sep 2022
28 Sep 2022
26 Sep 2022
3 Oct 2022
29 Sep 2022