Two-Sample Tests by using Stata

The remainder of this chapter draws examples from a survey of college undergraduates by Ward and Ault (1990).

About 19% of these students belong to a fraternity or sorority. On campus, these organizations and their members are commonly referred to as “Greeks” not with any reference to nationality, but because most of the organizations have names composed of Greek letters.

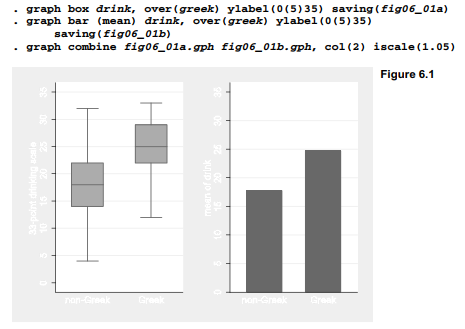
Another variable, drink, measures how often and heavily a student drinks alcohol, on a 33-point scale. Campus rumors might lead one to suspect that fraternity/sorority members tend to differ from other students in their drinking behavior. Box plots comparing the median drink values of members and nonmembers, and a bar chart comparing their means, both appear consistent with such rumors. Figure 6.1 combines these two separate plot types in one image, after using ylabel(0(5)25) to set a common y-axis scale for comparability.

The ttest command, applied earlier to one-sample and paired-difference tests, can perform two- sample tests as well. In this application its general syntax is ttest measurement, by(categorical). For example,

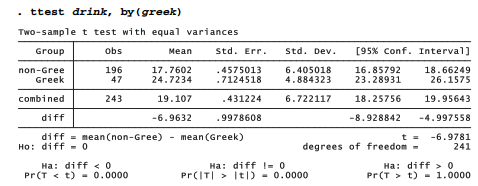
As the output notes, this t test rests on an equal-variances assumption. But the fraternity and sorority members’ sample standard deviation appears somewhat lower — they are more alike than nonmembers in their reported drinking behavior. To perform a similar test without assuming equal variances, add the option unequal:

Adjusting for unequal variances does not alter our basic conclusion that Greeks (fraternity/sorority members) and non-Greeks are significantly different. We can further check this conclusion by trying a nonparametric Mann-Whitney U test, also known as a Wilcoxon rank-sum test. Assuming that the rank distributions have similar shape, the rank-sum test indicates that we can reject the null hypothesis of equal population medians.

. ranksum drink, by(greek)

Source: Hamilton Lawrence C. (2012), Statistics with STATA: Version 12, Cengage Learning; 8th edition.