Developing and Articulating a Sampling Frame for Meta-Analysis

Given that meta-analysis uses the individual study as its unit of analysis, it is useful to think of your meta-analysis as consisting of a sample of studies, just as primary analyses sample people or other units (e.g., families, businesses) comprising its sample. In primary analyses, we typically wish to make infer­ences to a larger population that is represented by the sampled individuals; in meta-analysis, we typically wish to make inferences to a larger population of possible studies from the sample of studies included in our review. In both cases, we want our sample to be representative of this larger population, as opposed to a biased (nonrepresentative) set.

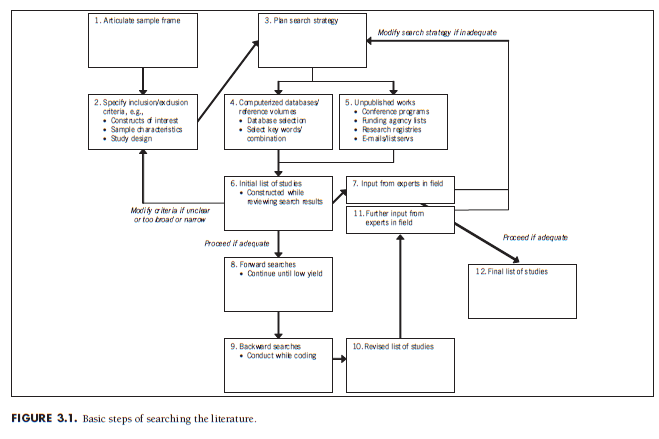
To illustrate the importance of obtaining an unbiased sample of studies, we can consider the threat of publication bias (discussed in further detail in Chapter 11). The top of Figure 3.2 displays a hypothetical population of effect sizes, with the horizontal (x) axis representing the effect sizes obtained in studies of this population and the vertical (y) axis representing the frequency that studies yield this effect size.¹ We see that the mean effect size in this population is somewhere around 0.20 and that there is a certain amount of deviation around this mean due to either sampling fluctuation or unspecified (random) differences. The bottom part of this figure shows the distribution of a biased sample of studies drawn from this population. I have used arrows of different width to represent the likelihood of studies from the population being included in this sample. The arrows to the right are thick to represent studies with large effect sizes being very likely to be included in the sample (i.e., very likely to be found in a search), whereas the arrows to the left are thin to represent studies with small effect sizes being very unlikely to be included in the sample (i.e., likely not found in a search). We can see that this differential likelihood of inclusion by effect sizes results in a biased sample. If you were to meta-analyze studies from this sample, you would find a mean effect size somewhere around 0.30 rather than the 0.20 found in the popula­tion. Thus, analysis of this biased sample of studies leads to biased results in a meta-analysis.

The goal of searching and retrieving the literature for a meta-analytic review is to obtain a representative, unbiased collection of studies from which inferences can be made about a larger population of studies. Meta-analyses differ from primary analyses in that your goal is typically to obtain all of the studies comprising this population as it currently exists.² Whether or not you are successful in obtaining all available studies (and it is not possible to know with certainty that you have), it is still appropriate to consider this set of studies as a sample, from which you might draw inferences about a larger population including studies you did not locate or studies performed in the future (assuming that these studies are part of the same population as those included in your meta-analysis).

This approach, in which you think of the studies included in your meta­analysis as a sample from a population to which you wish to make inferences, has two important implications. First, this conceptualization properly frames the conclusions you draw from results after completing your meta-analysis; this is important in allowing you to avoid either understating or overstat­ing the generalizability of your findings. Second, and more relevant during the planning stages of your review, this conceptualization should guide your criteria for which type of studies should or should not be included in your meta-analysis, as described next.

Source: Card Noel A. (2015), Applied Meta-Analysis for Social Science Research, The Guilford Press; Annotated edition.