Problem 7.3: Other Nonparametric Associational Statistics with SPSS

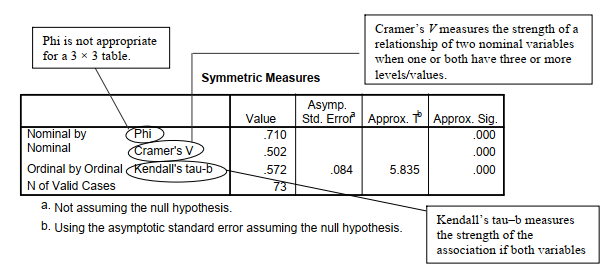
In addition to phi and Cramer’s V, there are several other nonparametric measures of association that we could have chosen in Fig. 7.2. They attempt, in different ways, to measure the strength of the association between two variables. If both variables are nominal and you have a 2 x 2 cross­tabulation, like the one in Output 7.1, phi is the appropriate statistic to use from the symmetric measures table. For larger cross-tabulations (like a 3 x 3) with nominal data, Cramer’s V is the appropriate statistic. Note that with a 2 x 3 or a 3 x 2 cross-tabulation, phi and Cramer’s V are the same. If the variables are ordered (i.e., ordinal), you have several other choices. We will use Kendall’s tau-b in this problem. The primary assumption of Kendall’s tau-b is that data are at least ordinal.

• What is the relationship or association between father’s education and mother’s education?

• Analyze → Descriptive Statistics → Crosstabs… 
• Click on Reset to clear the previous entries.
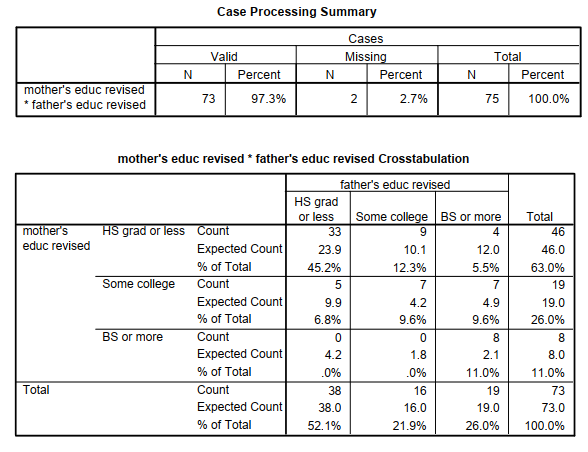
• Put mother’s education revised in the Rows box and father’s education revised in the Columns
• Click on Cells and ask that the Observed and Expected cell counts and Total percentages be printed in the table. Click on Continue and then
• Request the following Statistics: Kendall’s tau-b coefficient under Ordinal, and Phi and Cramer’s V under Nominal (for comparison purposes). Do not check Chi-square.
• Click on Continue then OK. Compare your syntax and output to Output 7.3.

Output 7.3: Crosstabs and Nonparametric Associational Statistics

CROSSTABS

/TABLES=maedRevis BY faedRevis

/FORMAT= AVALUE TABLES

/STATISTICS=PHI BTAU

/CELLS= COUNT EXPECTED TOTAL

/COUNT ROUND CELL.

Crosstabs

1. Not assuming the null hypothesis.
2. Using the asymptotic standard error assuming the null hypothesis.

Interpretation of Output 7.3

There are several nonparametric measures of association that we could have chosen from Fig. 7.2. All of them except chi-square attempt, in different ways, to measure the strength of the association between two variables roughly on the -1 to +1 scale used by the Pearson correlation (see Chapter 8). However, several of them, including phi and Cramer’s V, have maximum values considerably less than 1 under some conditions.

For tables with nominal data (like a 3 x 3 cross-tabulation of religion and ethnicity), Cramer’s V would be the appropriate statistic. In Problem 7.3, we requested Kendall’s tau-b because both mother’s education and father’s education are ordered variables and ordinal data. Cramer’s V (and phi) treat the cross-tabulated variables as if they were nominal even if they are ordered, so they would not be good choices for this problem. We requested them so you could compare them to Kendall’s tau-b.

If the association between variables is weak, the value of the statistic will be close to zero and the significance level (Sig.) will be greater than .05, the usual cutoff to say that an association is statistically significant. However, if the association is statistically significant, the p will be small (< .05). In this case, p is < .001 for Kendall’s tau-b, which is clearly significant, and the effect size (tau-b = .572) is large; the interpretation of tau-b is similar to that of r (see Table 6.5).

Example of How to Write About Problem 7.3

Results

To investigate the relationship between father’s education and mother’s education, Kendall’s tau­b was conducted. The analysis indicated a significant positive association between father’s education and mother’s education, tau (71) = .572, p < .001. This means that more highly educated fathers were married to more highly educated mothers and less educated fathers were married to less educated mothers. This tau is considered to be a large effect size (Cohen, 1988).

Source: Morgan George A, Leech Nancy L., Gloeckner Gene W., Barrett Karen C.

(2012), IBM SPSS for Introductory Statistics: Use and Interpretation, Routledge; 5th edition; download Datasets and Materials.