Certain numbers and number sequences are of special interest in wave theory. Of particular importance are the Fibonacci sequence and the related golden ratio.
1. Fibonacci
Leonardo Pisano, better known by his nickname Fibonacci, was born in 1170 in Pisa, Italy. Fibonacci’s father, Guilielmo Bonacci, was a public notary, working for the interests of the merchants of the Republic of Pisa. Because of Guilielmo’s work, Fibonacci traveled with his family extensively through Northern Africa and the Mediterranean as a child. At a young age, Fibonacci was exposed to the mathematical and accounting systems of the various merchants with which his father worked. In his writings, Fibonacci recalls learning the mathematical and accounting systems of India, Egypt, Syria, Greece, Sicily, and Provence.
Around the age of 30, Fibonacci ended his travels and returned to Pisa. There he wrote a number of important texts that played an important role in reviving ancient mathematical skills. Copies of his books Liber abaci (1202), Practica geometriae (1220), Flos (1225), and Liber quadratorum (1225) still exist today. Other books written by Fibonacci, such as his book on commercial arithmetic, Di minor guisa, have been lost.
The writings of Fibonacci are credited with bringing the Hindu-Arabic decimal place mathematical symbols that we use today to Western Europe. Many of his works dealt with pricing issues faced by merchants. He is thought to have invented present value analysis of cash flows in contracts and a method for expressing investment returns. In addition, he solved a number of complex interest rate problems (Goetzmann, 2003). Fibonacci was likely the world’s greatest mathematician in his time. Although his work formed the basis of our decimal system and he laid the groundwork for financial mathematics, he is unfortunately remembered today almost exclusively for a small portion of his life’s work——his numerical sequence.
2. The Fibonacci Sequence
Fibonacci derived the sequence by answering the question of how many rabbits can be produced over a year from an original pair, in an enclosed space, when all pairs give birth each month to a new pair that in turn can breed in two months. The sequence of pairs occurs in the following manner by month: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and 144. These are called Fibonacci numbers. Fibonacci numbers are simply a sequence in which the last number is added to the previous number to arrive at the next number. For example, 5 plus 3, the previous number, produces 8, the next number; next, 8 plus 5 produces 13, the next number. This sequence can continue to infinity.
3. The Golden Ratio
There are a number of reasons why this sequence is of interest to mathematicians and scientists. One reason is the relationship that the sequence has to the “golden ratio.” Except in the very low numbers, the ratio of any number in the sequence to the next lower number is 1.618 (for example, 144/89 = 1.61798); the ratio of any number in the sequence to the next highest number approaches 0.618 (for example, 55/89 = 0.61798). The number 1.618, known as the golden ratio, and its reciprocal of 0.618, possess many interesting properties. For example, it is the only number that when added to 1 is the same as 1 divided by itself. Another fascinating fact is that 1.618 multiplied times 0.618 = 1. There are many more strange relationships between .618 and whole numbers; see Box 20.1 for a demonstration of the “mystery” of this number. Mathematicians use the Greek letter phi to refer to this ratio.
The golden ratio has been of interest at least since the pyramids were built and likely long before. Buildings built in proportion to the golden ratio were thought to be most pleasing to the eye. The Parthenon and the Washington Monument, for example, have dimensions based on the golden ratio. Not until relatively recently, in terms of the history of civilization, was the golden ratio derived mathematically through the Fibonacci sequence.

Plato considered the golden ratio to be the “most binding of all mathematical relations and considered it the key to the physics of the cosmos” (Frost and Prechter, 2000, p. 101). German-born seventeenth-century mathematician, astronomer, and astrologer, Johannes Kepler likened the golden ratio to a fine jewel and claimed that it described all creation. The reason for this adoration is that the ratio appears in innumerable natural phenomena. For example, consider a spiral that has its arc length to its diameter at a ratio of 1.618; this spiral occurs in nature in comet tails, galaxy spirals, spider webs, pine cones, snail shells, ocean waves, and even the human finger when curled. It is universal. It is a growth pattern in nature, and Elliott hypothesized that it occurred in the stock market as well.
Look back at Figure 20.1; see how the number of waves, as the pattern becomes more complex, follows a Fibonacci sequence. The first waves are corrective and impulse, one and one, totaling to two. Then there are three corrective waves and five impulse waves, totaling eight waves. Each of these numbers is part of the Fibonacci sequence. If we take the progression further and include smaller and smaller waves, the number of waves continues in a Fibonacci sequence. Although this relation to Fibonacci numbers is interesting, it is portraying the ideal. But remember if you take any two whole numbers and add them together, then add to the sum the previous highest number, eventually you will arrive at phi, the Fibonacci ratio (1.618), between the highest number and the previous highest number. (See the example in Box 20.1.) Thus, the ratio is the universal relation rather than the numbers themselves. It is the ratio and derivatives of it that are applied to stock markets.
4. Price and Time Targets
Elliott wave enthusiasts, to predict retracements and price targets, as we have already seen, and to project the timing of the next series of waves, use Fibonacci ratios. For example, Prechter notes that corrective waves tend to correct approximately 61.8%, or its complement 38.2% (100% – 61.8%), of their corresponding impulse waves. Prechter is quick to point out, however, that this is a tendency, not even a guideline, and is not dependable. He found that more reliable relations exist in projecting target prices for alternating waves. For example, in percentage terms, impulse waves tend to be related in some manner by 2.618, 1.618, 0.618, or 0.382 As an example, he noted that the rise in the Dow Jones Industrial from the low in 1932 to 1937, wave 1 gained 371.6%, whereas wave 3 from 1942-1966 gained 971.7%, 2.618 times as much. This relationship is pictured in Figure 20.11.

Numerous other examples of relations between waves can be cited. One common occurrence is when wave 1 and wave 5 are the same length, wave 3 is often either 1.618 or 2.681 times wave 1. In addition, in a fifth wave extension, the length of the fifth wave is frequently 1.618 times the length from the beginning to the end of wave 3. Many times in an extended wave 1, the remaining four waves end at 0.618 the length of the extended first wave. In corrective waves, wave C is often related to wave A in some Fibonacci ratio, and the wave 4 length is often related by a Fibonacci ratio or by equality to the length of wave 2.
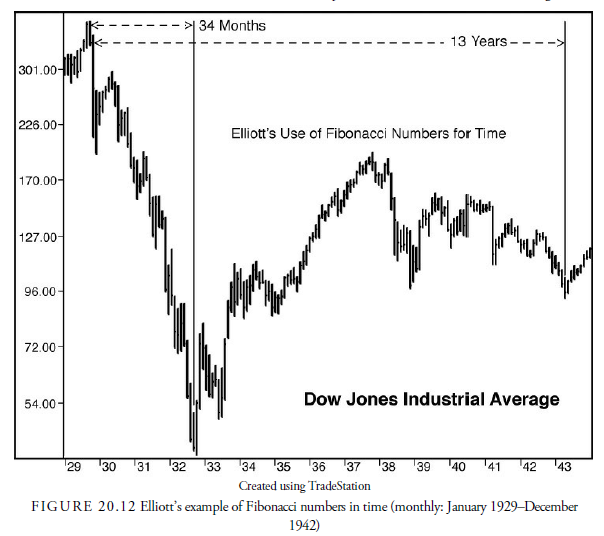
In addition to the extent of price movements in waves being related by Fibonacci numbers, times in stock market data have been related to the Fibonacci ratio. However, this exercise is spurious at best. Tables are often used to show the time differences between important peaks and valleys in market prices that occurred in a Fibonacci number of years, months, or days. Elliott himself used the example of the 34 months between the peak in September 1929 and the bottom in July 1932 and the 13 years between the peak in 1929 and the low in 1942 (see Figure 20.12). Although others also have seen a relation between Fibonacci time counts and important events, Hamilton Bolton, a contemporary of and correspondent with Elliott, and publisher of the Bank Credit Analyst, stated, “Permutations tend to become infinite” (Frost and Prechter, 2000, p. 141). One of the tenets of any technical theory is that the principles must make sense. In the case of time, which is determined somewhat arbitrarily by humans and differently over the ages, the likelihood of there being a consistent series of time intervals that follow Fibonacci sequence numbers is a little far-fetched. Indeed, a comprehensive study by Herbert Riedel, PhD (1989) on 182 days of the Dow Jones Industrial Average in 1985 demonstrated that no evidence of Fibonacci ratios was present either in retracements or in timing.
Although there is perhaps a far-too-often coincidence of waves being related to other waves by some variations of the Fibonacci ratio, the practical problem is that the relations, even if valid, are not usually known until after the fact. Thus, the relations are interesting but generally unproductive. To some extent, the same can be said about wave structure. One of the great problems with Elliott wave analysis is that the proper sequence of impulse and corrective waves is not often recognized until after the price action has completed. Even then, analysts—even those with considerable experience—will argue over whether the configuration is one type or another. For the technical analyst, especially one starting out, the concept of the Elliott Wave Theory must be understood in general terms, but the likelihood of being a seasoned practitioner is remote without considerable study, analysis, memorization of the rules and guidelines, and inspection of many long- and short-term price charts.
5. W.D. Gann
William Delbert Gann, born in Texas in 1878, roughly at the same time as Elliott, left his formal schooling at the age of 16 to begin his career as an itinerant salesman. Legend suggests that he made several fortunes in the commodities markets, married a number of younger women, and spent huge sums on planes, yachts, real estate, and gambling in Cuba (Costa, 2000). Some believe he was a scoundrel, that his courses on trading were full of generalities and astrology, and that he sold his advisory service several times (Williams, www.ireallytrade.com/asiseeit.htm). We do know that he died with few assets. Nevertheless, Gann was a prolific writer, both of novels and advisory books. He published articles and sold courses on trading. Richard Wyckoff wrote an article on his trading, and Gann received considerable notoriety in his time for trading, especially in cotton. He was a superb trader, as witnessed by several independent observers. Whether or not he used the methods he proposed is uncertain.
Gann’s published concept of market structure, specifically in commodity markets, encompassed time as well as price. He is known for such things as circles, squares, and triangles, all having to do with the angles of a circle. For example, he strongly believed in the seasonal cycle of approximately 360 days, the same as the number of degrees in a circle, the circle of the earth traveling around the sun. Thus, portions of a circle were important, such as 90, for 90 degrees, a quarter year, and 180, a half year; he expected that lows to highs or highs to lows would generally occur within those time periods or divisions of them. He preached that the range between tops and bottoms could be divided into zones that would project retracement levels, and he used angles drawn from tops and bottoms that, when crossed, especially at the same level as his support and resistance zones, were important predictors of time and price for retracements. His concept of squares and rectangular shapes, not mathematical formulas, defined where in time and price future price motion should occur. Gann also discovered the strength of the fifth year of each decade, which since 1905 has been an up year. He claimed incorrectly to have invented swing charts, but he did successfully promote them as a method of trend following. His square of 52 is based on the 52 weeks in a year, which he called a circle. His square of 144 is 12 times 12, or the number of months in a circle. He devised spiral calculators such as the square of nine, the square of four, the 360-degree circle chart, and the hexagon chart. Gann also published a summary of 28 trading rules, all of which are still valid today.
There is no question that Gann was an inventive person. Whether his discoveries are hocus-pocus to sell his courses and books we do not know because his methods are too vague to properly test, but even today a few analysts follow his numerological methods and claim success.
Source: Kirkpatrick II Charles D., Dahlquist Julie R. (2015), Technical Analysis: The Complete Resource for Financial Market Technicians, FT Press; 3rd edition.

exceptional post