What About Market Efficiency?

Because of the central role the EMH has played in financial theory in the past 50 years, we spend a little time developing the basic ideas of the EMH and how, although it might be an interesting and thought- provoking model, it does not describe the real world of investments and markets.

Market efficiency is a description of how prices in competitive markets respond to new information. The arrival of new information to a competitive market can be likened to the arrival of a lamb chop to a school of flesh-eating piranha, where investors are—plausibly enough—the piranha. The instant the lamb chop hits the water, there is a turmoil as the fish devour the meat. Very soon the meat is gone, leaving only the worthless bone behind, and the water returns to normal. Similarly, when new information reaches a competitive market, there is much turmoil as investors buy and sell securities in response to the news, causing prices to change. Once prices adjust, all that is left of the information is the worthless bone. No amount of gnawing on the bone will yield any more meat, and no further study of old information will yield any more valuable intelligence. (Higgins, 1992)

The EMH, which evolved in the 1960s from Eugene Fama’s PhD dissertation, assumes that at any given time, security prices fully reflect all available information and that prices are at equilibrium. The implication of this hypothesis is that if current prices fully reflect all information, the market price of a security is an unbiased estimate of its value, and no investment strategy can be used to outperform the market.

The basis for the EMH is the economic theory of competitive markets. Basic economic theory teaches that investors have rational expectations and that through arbitrage competition will create in aggregate an efficient market. As new information enters the marketplace, so the hypothesis states, investors will become aware of it and immediately will act rationally to adjust the price to the new equilibrium value of the security. Should the price deviate from its true value, so-called “noise,” arbitrageurs will compete to bring that price back to that value at which the price will be in equilibrium with its value. Such is a purely efficient market. No investor has an advantage over another, and thus both technical and fundamental analysis is futile. Figure 4.5 shows what would happen in a purely efficient market to a security price upon the announcement of new information. It shows a step-like progression as the price reacts instantly to that new information.

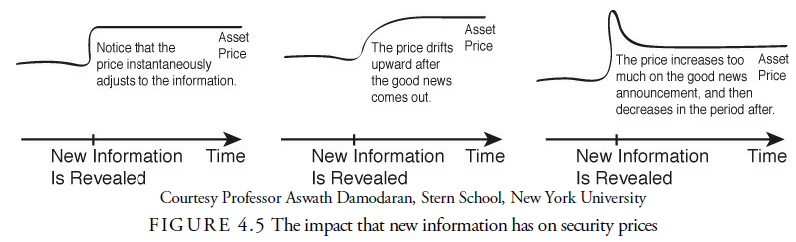
This figure shows the ideal efficient market assumption of how information affects price and two other assumptions that have been shown to be more realistic.

1. New Information

Information for purposes of the EMH is any news that will affect the equilibrium price of the security. In the case of a stock, most analysts and theoreticians hypothesize that the value of a company’s stock is equal to the present value of the future cash flows that the investor purchasing the stock expects to receive. This present value is a function of all of the company’s future cash flows and the expected risk-adjusted interest rate during the period that the cash flows occur. New information is any news that affects interest rates or cash flow directly or indirectly. That information can be related to the underlying company or can be any of a multitude of other news about the economy, politics, and so on. In short, it can be almost anything because almost all change has an effect on value regardless of its immediate importance.

Information itself is problematic. It is far from true that all investors will receive new information instantly, that they will react rationally and immediately to that new information, and that arbitrageurs will immediately and always act to adjust any deviations in the price back to its new equilibrium value. Indeed, in their 1980 article “On the Impossibility of Informationally Efficient Markets,” Stanford Grossman and Joseph Stiglitz argue that because information is costly for investors to obtain, prices cannot perfectly reflect all available information. If prices do perfectly reflect all available information, those who obtain costly information receive no compensation for doing so.

A well-documented characteristic of financial markets is the presence of asymmetric information. Asymmetric information refers to a situation in which one party of a transaction has information that the other party involved in the transaction does not have. For example, the managers of a corporation have better information about how well their business is doing than the stockholders do. In addition, the company managers know whether they are being honest about their reporting of the company’s financial position, but stockholders cannot immediately discern whether the managers are being honest.

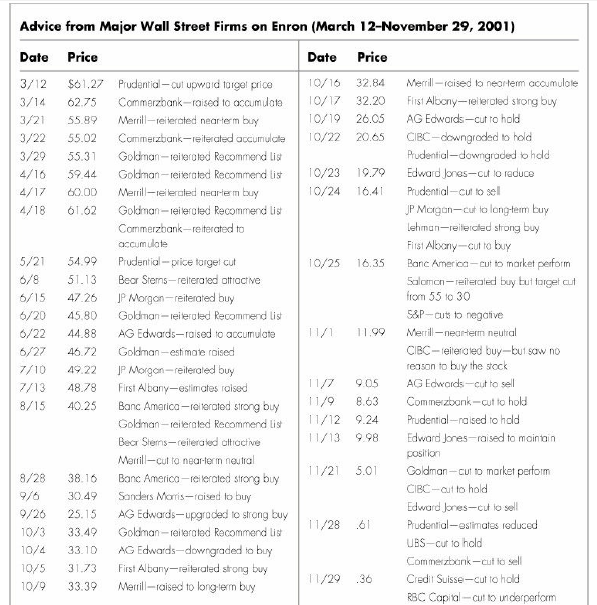
As any investor knows, in the real world, all information is not disseminated instantly to all market players. A classic example of the presence of asymmetric information is the Enron debacle in 2000. The management of Enron knew for years that the fundamental numbers being reported to the public and to analysts were incorrect and were upwardly exaggerated to maintain an artificially high stock price for acquisitions (see Figure 4.6). The true information was kept inside the corporation and known by only a few insiders.

F IG U R E 4.6 Point and figure chart of Enron stock price March 2001 through November 2001, with samples of Wall Street advisory comments on specific dates

Even when the real story began to leak out and the stock price began to decline, security analysts on Wall Street continued to recommend the stock based on projections from the old, incorrect numbers. Thus, this new information was dribbled out to the public in small amounts. But even when finally disseminated among analysts, it was not interpreted correctly. This is an extreme case, of course, but in the practical world of investments, new information is disseminated slowly through the investment world and is acted upon with even more hesitation.

Therefore, several problems exist in the process of information dissemination. First, in its transmission, the information might be inaccurate. Second, the source might be intentionally lying, as in the case of Enron executives. Third, the information might not be disseminated immediately even though it is time sensitive. Fourth, there exists a natural lag between when the news is announced and when it is received by the last recipient, during which time the information might have changed.

Once information disseminates, the market participants must interpret it. This interpretation can be extremely difficult. The information might be too numerous and too complex and, thus, not easily or inexpensively interpreted. The information age produces an enormous and incomprehensible amount of news and data that is impossible to assimilate. Often, information is vague and its consequences not understandable. Not enough precedent has occurred to be able to judge what potential consequences are likely from specific information. In short, information by itself is unreliable and its interpretation subject to logical errors.

Academic studies suggest that it would be extremely costly for market participants to attain and assimilate perfectly new information. In his book A Theory of Adaptive Economic Behavior, Cross (1983) discusses the costliness of solving the complex statistical problems that modern economic and financial theory assume that individuals in the market are working.

The methodological price for this approach [traditional statistical and mathematical decision analysis] has been extremely high, however, for it has become necessary to assume individuals in these markets can be represented as mathematical statisticians capable of solving specific problems that are often beyond the analytic abilities of professionals in that field. It also requires reliance on the assumptions that individuals follow optimizing rules of behavior under just those dynamic and risky types of situations for which the assumption of optimization has the least empirical support. (Cross, 1983)

Some of the optimization problems that market participants would need to be solving are beyond the analytical abilities of professional statisticians using high-speed computers. G. Hawawini and D. Keim (1994) argue that markets are not efficient because investors are prevented from optimizing by their inherent cognitive limits. Rode, et al., in a Wharton School working paper (1995), argue that there are “substantial constraints on the information processing time allowed,” that “there is also a continual abundance of new information made available,” and that “this flow of information easily exceeds investor’s abilities to process it completely.” They argue that because the object of technical analysis is to make sense out of this complex world of new and continual information, it has created rules that substitute simplified and “less complex for the intractable.” Basic economic theory teaches that market players will continue the costly process of gathering and processing information only so long as the cost of doing so is less than the cost of being wrong. Technical analysis represents a rational choice for bounded rational investors; it can allow them to make reasonably well-informed decisions with relatively small information processing costs.

Interpretation is also subject to changes in risk preferences. In his 2004 article “The Adaptive Markets Hypothesis: Market Efficiency from an Evolutionary Perspective,” Andrew Lo argues that even in the rational market assumed in the EMH, risk aversion is not a constant. Risk aversion depends on the history of market behavior, and, thus, may be time varying. For example, an investor who had never experienced a stock market collapse before might assume a different risk preference structure after losing money in the 1987 crash or the 2007-2009 decline than she had before. This means that even under a rational decision-making assumption, the risk parameters are not constant. Time-varying risk assumptions can also develop when investors trade based on irrational expectations, and time-varying risk assumptions may arise from the interactions of heterogeneous investors. In short, the assumption that risk assessment is a constant is invalid.

2. Are Investors Rational?

This brings us to the subject of rationality. The EMH assumes that investors as a group will act rationally. In its more recent version, it also assumes that there are irrational participants, called “noise” players, in the marketplace (Black, 1986). When noise players, who drive prices away from intrinsic value, are not counteracted by arbitrageurs, who are called “informed” players, the market is considered irrational. Thus, individual irrationality can exist in the marketplace, but it is usually nullified by rational arbitrage.

We will get to the subject of arbitrage shortly, but first let us look at the critiques of rationality. Most have centered on the subjects of behavior and preference of market participants.

Market participant actions depend on how individuals process information and make decisions. Information interpretation and decision making are subject to cognitive bias and limits. Behavioral finance and neurofinance study the irrational and often unconscious behavior of investors and how they interpret information. Some of the results have shown illogical behavior that would be undesirable in the marketplace, such as comfort in crowds called “herding” (Huberman and Regev, 2001), overconfidence based on little information (Fischoff and Slovic, 1980; Barber and Odean, 2001; Gervais and Odean, 2001), overreaction (De Bondt and Thaler, 1985), psychological accounting (Tversky and Kahneman, 1983), miscalibration of probabilities (Lictenstein et al., 1982), hyperbolic discounting (Laibson, 1997), and regret (Bell, 1982; Clarke et al., 1994). More and more of these kinds of studies are demonstrating that investors often act irrationally or unconsciously.

Preference in markets is directly related to the assumption that investors are risk averse. The EMH assumes that investors will be willing to take on more risk only if they are compensated by receiving a higher expected rate of return. Thus, the EMH assumes that investors will optimize their decisions based on their perception of and ability to assume risk. Many psychologists and experimental economists have found empirically “specific behavioral biases that are ubiquitous to human decision-making under uncertainty, several of which lead to undesirable outcomes for an individual’s economic welfare…” (Lo, 2004).

The most famous early experiment was by Daniel Kahneman of the University of British Columbia and Amos Tversky (1979) of Stanford in which a number of participants were asked about preferences for different probability costs and outcomes. Invariably, they chose, when presented with potential gains, a risk- aversion strategy, and when presented with potential losses, a risk-seeking strategy. In the financial markets, this kind of decision making can be disastrous. It suggests that investors have a strong tendency to sell winning positions and to keep losing positions, quite contrary to the rationality assumption of the EMH. For the duo’s work in behavioral finance, Kahneman received the Nobel Prize for Economics in 2002. Unfortunately, Tversky died in 1996 and was, therefore, ineligible.

Advocates of the EMH argue that although irrational players can sometimes affect prices for a short time, prices are quickly brought back into equilibrium to their true value by a rational arbitrage that profits at the expense of the players with irrational beliefs. Thus, prices may stray from their true value occasionally but will quickly return to them. The stray prices are “noise” about the true value and provide opportunity for the insightful arbitrageur. Prices always return to their true value, and irrationality, although it does occur, is never in control of prices because profitable, competitive arbitrage will always return those prices to their true value.

This brings us to the question of whether arbitrage actually does bring prices back to equilibrium or whether there are other forces, of human bias, emotion, or physiology, that can overwhelm the rational force of the arbitrageur.

3. Will Arbitrage Keep Prices in Equilibrium?

Price equilibrium at the intrinsic value of a security in the EMH relies on arbitrageurs acting on a profit motive to bring prices back to equilibrium if they should stray. In practice, the ability for arbitrage is less likely than the EMH assumes.

Ideally, risk-averse arbitrage is “the simultaneous purchase and sale of the same, or essentially similar, security in two different markets at advantageously different prices” (Sharpe and Alexander, 1990). In many market instances, there is no substitutable alternative for the arbitrageur, or arbitrageurs are unable to trade alternatives for practical reasons such as lack of liquidity, lack of margin, trading costs, and so on. Arbitrage depends on sufficient liquidity for the arbitrageur to get into a position and, most important, to get out. In periods of fast markets and emotional panic, liquidity is often absent, leaving the risk to the arbitrageur that a position cannot be closed. Trading costs, in addition to slippage from illiquidity, are a concern to the arbitrageur. Trading costs must be minimal because with the small spreads involved, they can reduce a large portion of potential profit. These factors of liquidity and costs often convince the potential arbitrageur to go elsewhere to make a profit.

When there is no substitutable alternative for arbitrage, one side or the other of a run away from the theoretical intrinsic equilibrium value can continue. There is nothing to check it. In the absence of a tradable vehicle, no tool is available to provide a risk-averse arbitrage. This is true, for example, in the entire stock and bond market. If “irrational exuberance”¹ (a term used by Yale Professor Robert Shiller) develops, as it did in the 1920s, 1990s, and 2000s, and prices rise significantly above their equilibrium value, there is no security that arbitrageurs can use to arbitrate prices back to their rational value without incurring substantial capital risk. Without an arbitrage vehicle, prices can trend in one direction without the arbitrage check to bring them back to rational values.

“Shiller used the phrase during testimony before the Federal Reserve, and Alan Greenspan repeated it in his famous December 1996 speech.” (Interview of Professor Shiller by Chris Rugaber, Motley Fool [Fool.com], April 11, 2001.) The apparent origin of the phrase, however, goes back to Hamilton (1922).

As opposed to the EMH, technical assumptions include the ability for prices to trend, in which case the arbitrageur, if he exists, may be overwhelmed by and may even join the consistent trend of prices away from true value. In addition, when a trend is completed and reverses, researchers such as De Bondt and Thaler (1985) empirically observe that those prices often trend in the opposite direction well beyond rational value. This cyclicality in price direction and extent is assumed by technical analysis to be due to irrational behavior overcoming rational arbitrage.

Box 4.2 A Case Study in the Failure of Financial Theory—The Long-Term Capital Management Debacle

The failure of rationality and arbitrage in the face of irrational behavior was empirically but unfortunately demonstrated by the collapse of Long-Term Capital Management (LTCM) in 1998. Managed by extremely knowledgeable and sophisticated professionals, this fund had two Nobel Prize winners, Scholes and Miller, on its advisory staff. It leveraged itself by avoiding Federal Reserve margin requirements and otherwise sane ratios of safety into almost 30-to-1 positions of investments to cash and controlled thereby more than 300 billion dollars’ worth of arbitraged positions. In addition, it held more than a trillion dollars in derivative obligations that, had they failed, would have brought that amount of exposure to otherwise secure positions in the banks that were on the other side of these contracts, and it would have forced them to liquidate also. In other words, LTCM was in a position to bring down the U.S. and perhaps world financial system if it failed.

One of the problems of pure arbitrage is that the marketplace, over very short time periods, is efficient enough that bid-ask spreads are extremely small and the potential profit so minimal that meaningful profit can only come from a very large position, similar to a grocery store making many small profits on high turnover. Leverage must then be used to increase the size of the position. The danger is that although leverage can increase profit, it can also increase the risk of capital loss to the point at which, depending on the size of the leverage, a small movement against a position can wipe out the underlying assets. With a 30-to-1 leverage and 300 billion in contracts, a move of only 3.4% against the positions would be enough to wipe out the fund and force liquidation. This is essentially what happened to LTCM.

Here was a portfolio managed on the most modern versions of finance theory that collapsed because certain unrealistic assumptions were made, based on the EMH, and where “mispricing” became worse before it became better, forcing the covering of positions at the worst time and thus exacerbating the mispricing even more.

Investors flocking to safety and liquidity in the aftermath of the Russian (debt) default in August 1998 were stronger, at least for several months, than the forces of rationality. (Lo, 2004)

Thus, even when a series of theoretically riskless spread positions were entered with rational expectations, the reaction to an event overwhelmed those positions, and lack of liquidity as well as the pressure of margin calls created a substantial collapse. Finally, several major banks and brokerage firms, with the insistence and support of the Federal Reserve, had to take over the assets of LTCM, force it out of business, and gradually liquidate its positions over time as the market spreads improved.

The lesson learned from this expensive adventure into the EMH was that market forces may abide by the principles of efficiency a majority of the time, but occasionally and unexpectedly, irrational forces can overwhelm rationality and cause a disaster. Several months after the LTCM debacle, arbitrage professionals analyzed the LTCM portfolio and agreed that the positions were reasonable, and after a time the spreads initiated did return to their mean. In other words, had LTCM not been so highly leveraged and had it been able to withstand the short-term losses, it would eventually have profited. To achieve a high return on capital, however, LTCM needed leverage. Leverage introduced another risk, over the risk of volatility —the risk of ruin. And when the markets ran outside the normal distribution of returns and developed a “fat tail,” LTCM was out of business. This is why the assumption of a normal distribution in price returns can be hazardous. It is also why the subject of behavioral finance was born.

Fortunately for technical analysis, empirical evidence of EMH demonstrates that its core assumptions, as shown earlier, have severe shortcomings. The validity of the hypothesis lives or dies with its assumptions, but the specific EMH assumptions cause a circular logic that cannot be proven in real terms and allow the subject of finance to avoid the embarrassment of empirical evidence proving it wrong. Indeed it cannot be proven right or wrong.

Fortunate in some ways for the academics is the Joint Hypothesis Problem as it applies to EMH because it frees them from having to prove it. This logic problem says that the EMH can never be disproved. It is based on the requirement for an acceptable test to include a model of how prices may be established efficiently. (There are too many factors, and each must have a rational basis.) Because there is no such acceptable model, the hypothesis is untestable. This puts it into the category of a religion where theory cannot be tested. As a religion it is promulgated purely on belief, not factual evidence, and thus believers still preach it to innocent, uniformed finance students.

Source: Kirkpatrick II Charles D., Dahlquist Julie R. (2015), Technical Analysis: The Complete Resource for Financial Market Technicians, FT Press; 3rd edition.