A Model of Perceptual Geometry in Phenomenology

Brentano’s reference to Beltrami raises an important question. In a conven­tionalist account of non-Euclidean geometries, the meaning and intuition of geometric concepts varies given the interpretation in a model. If it allows consistent deductions, the intuition needs to be adjusted to the interpretation of the model. Poincare (1898: 1) claimed that “sensations cannot give us the no­tion of space” and that “sensations themselves have no spatial character.” The space results from understanding that sensations change as one moves and that these changes can be inverted through compensating movements. He sug­gested that because of acquired experience or evolution, human beings have selected the mental compensations corresponding to the Euclidean space. Yet there is no reasoning or experiment to decide whether these mental compen­sations or others, corresponding to a non-Euclidean space, are appropriate to the external world. This account may be legitimate in terms of the theory of knowledge but it has essential implications also for the theory of perception. As previously shown, Beltrami built models to find the surface in the Euclidean space with the suitable properties onto which a part of a non-Euclidean space could be mapped and visualized. In fact, Beltrami himself showed that there is no Euclidean visualization for the whole three-dimensional non-Euclidean space, and Hilbert (1901) later proved that no surface in the three-dimensional Euclidean space can map even the whole non-Euclidean plane. Still, Beltrami’s point according to which the mapping, albeit of a single region, should yield something spatial with the right observable properties remains valid. What would a perception of such a space within the model be? The question relies on a theory of the ordinary perception of the spatial properties of bodies.

Von Helmholtz (1870, 1878) addressed the problem within the framework of the question about the origin of the concepts of geometry and the relation between perception and geometry of physical space, with particular reference to those concepts allowing the construction of rigid bodies. He considered a model that maps the Lobachevsky hyperbolic space onto a Euclidean sphere (see Beltrami, 1868/1869). In this model a mobile straight line of constant length corresponds to a straight line whose length changes as a function of the motion to the center or the surface of the sphere according to a general law. Thus the deformation of all bodies depends in the same way on their position; hence, the relative rigidity of two bodies is preserved. A yardstick is not rigid in the usual sense, yet two bodies undergo the same deformation so that in every experiment requiring measurement by coincidence they will be found to behave like rigid bodies with respect to each other. Then what about the ap­pearances of these relatively rigid bodies, as well as the possibility of making visual judgements of measure (Augenmafi)? Von Helmholtz suggests that if we could look inside the sphere through a transparent region of its surface, we will see the bodies deforming while moving, provided that the deformations have sufficient magnitude to be seen. However, suppose that we too are in­side the model and that our bodies undergo the same deformations or, at least, that their appearances give us no clues for the perceptual judgements we are accustomed to make in our physical world. If perception were bound to the form of Euclidean space, the bodies would not appear rigid while moving. We would keep on perceiving Euclidean bodies that are, however, deformed as they move. Instead, if perception can wean itself from the usual perceptual judgements and get into the habit of new ones, like when one adapts to convex or concave lenses, the bodies would appear absolutely rigid and deformations would no longer be apparent. Thus, the bodies in the Lobachevsky space yield not only the same measurements but also appearances equally as adequate as the usual Euclidean space. If the adaptation did not succeed in freeing one completely from being Euclidean, the new appearances would be equivalent to a sensory illusion which the subjects would get rid of, like they do for the apparent movement of the sun.

Gerhards (1932, 1936) remarks that although a Beltrami sphere cannot be built in our world, a similar construction can be realized by presenting a se­quence of drawings through cinematographic or stroboscopic motion. He cites Cayley (1859) and Klein (1871), who proved that the law of deformation of the Beltrami model admits of a more general form and that the sphere can be visu­alized as compressed into an ellipsoid. Thus if drawings of configurations with the desired spatial properties are realized, joined to one another in sequence and presented through a cinematographic projection or the stroboscope, the subjects can see moving non-Euclidean figures as if they were placed inside the Euclidean map yielded by the projection (Gerhards, 1932: 927, 1936: 438, for details). It is possible thus to observe whether or not the deformations are no­ticed as such and to what extent, and to determine their perceptual meaning.

In a first experimental set carried out through the cinematographic pro­jection, Gerhards uses a disc and a sphere in the Lobachevsky space, whose Beltrami model is built according to the Cayley and Klein projective interpre­tation. The model of a Lobachevsky disc S with eight uniformly distributed diameters is a disc S’ with eight chords intersecting at an eccentric point P’. If S rotates on its plane around the middle point, the model S’ undergoes a deformation that Gerhards calls “quasi-rotation”: P’ remains fixed, while the eight chords change their length periodically. He reports that in the quasi­rotation shown in the movie, subjects see a sort of “visual paradox” from the Euclidean standpoint: the eccentricity of P’ is clearly seen, but at the same time S’ appears globally rigid (1932: 927). The same visual paradox occurs with a Lobachevsky sphere K with eight uniformly distributed meridians around an axis A. If K rotates around A and the rotation is shown in a movie, K appears as an ellipsoid K’ that realizes a quasi-rotation around the eccentric axis A, al­though at the same time it appears globally rigid. In the second experimental set carried out through the stroboscope, Gerhards first uses a configuration of four points P_i(_1-4) that are laid eccentrically to an internal point P (see figure 36a). He draws sixteen variants of this configuration by shifting the place of P_i(_1-4) counterclockwise by a 90°/i6 angle. The variants are inserted in a clock­wise order in the stroboscope so that when viewed through its slits, a configu­ration G₁ of points is seen to realize a quasi-rotation in which P remains fixed while the four points considered with respect to P run with the same angular velocity along the elliptical trajectory E (see figure 36b).

The Euclidean distance from P_i to P is found to change periodically dur­ing the quasi-rotation, being greatest on the left of P and smallest on its right; hence, from the Euclidean standpoint G₁ undergoes a deformation. In fact G₁ might be a section of infinitely many ellipsoids, each with its own law of de­formation, in which G₁ could remain rigid while moving in the non-Euclidean quasi-rotation. Yet when G₁ is seen through the stroboscope, it does not appear rigid. If one of the P_i is tracked while looking also at P, the point appears to move toward and away from P. In this case, perception conforms to the Euclid­ean standpoint because the configuration that is rigid in non-Euclidean space is perceived to be deforming while moving. However, G₁ is weakly character­ized as a perceptual figure. It is interesting to consider what happens if the configuration is modified so that one is more likely to see in it an organized self-contained figure. Gerhards adds some straight lines to the configuration of points to obtain a new figure G₂,which can be reproduced in figure 37 (the elliptical trajectory is still drawn in the figure for the sake of the reader).

When G₂ is seen to move through the stroboscope, it appears rigid, looking like a wire wheel that is slightly slanted with respect to the frontal plane. The left side appears to point forward, the right backward. Therefore strengthening the characterization of G₁ as a figure brings about the appearance of a rigid body, which nonetheless would present a visual paradox if it were considered as if perceived from the standpoint of the Euclidean space. To be sure, the wheel appears rigid and slanted, but it also presents features that would be inconsistent with the appearance it could bring about in the Euclidean space. If the corresponding Euclidean figure were seen from above and a bit slanted, its spokes would have the same Euclidean length, and while the fulcrum P of the slant would still be located eccentrically to the elliptic contour it would now be lying on the minor rather than the major axis (figure 38 is an instance of what it would be like).

Still, if one looks at G₂, trying once again to isolate a line along with the pair of points laid on it while also keeping P in sight, the configuration undergoes a deformation. Gerhards report that subjects see either the points moving to­wards and away from P or the line shortening and lengthening itself. Will this deformation still occur if G₂ is characterized further as a figure, thus giving rise to a new configuration G₃? A configuration similar to the one presented to subjects by Gerhards is figure 39.

If G₃ undergoes the quasi-rotation and the subject is asked to track a single spoke, the spoke no longer appears to be shortened and lengthened. Instead, the figure appears absolutely rigid. G₃ does not appear flat like the wire wheel in G₂, rather as a three-dimensionally rotating rigid cone or as a conic screen, whose apex P verges either before or, if seen inverted, behind the plane of the elliptic contour. One of the deformations seen in G₂ may still occur but it does not appear to be real, rather it looks to be a perspective distortion. Conse­quently one may conclude that G₃ appears rigid rather than deformed because it is a stronger figure than G₂. Once again Gerhards emphasizes that G₃ does not present the aspect of a slanted Euclidean cone, which indeed would look as figure 40 (compare it with figure 38).

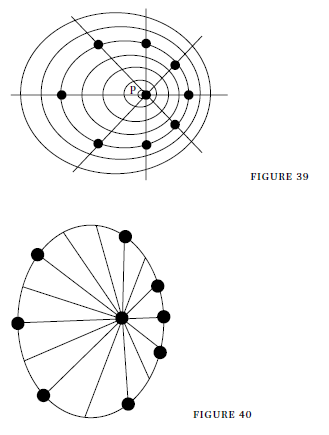
In comparison with G₃ the peak P is a bit displaced on the minor axis of the elliptic contour and the spokes have a different localization on the outer surface.

Gerhards points out that it might still be possible to consider a single draw­ing of G₃, among those that make the sequence that yields its perception, as the slanted section of a circular cone as it would appear from a viewpoint lying above on its axis. Yet he remarks that an actual rotation of such a cone should yield a view different from G₃ because any point of the spokes on the surface, if seen frontally, should draw a Euclidean circle around P, thus moving away from the elliptic trajectory that is in reality given in the quasi-rotation. This means that if even a single drawing of G₃ were perceived from a Euclidean stand­point, it would undergo a considerable deformation. However, unlike what one expects on the grounds of von Helmholtz’s reasoning, this Lobachevsky configuration is seen as rigid even at first blush. In general, the configurations appear more rigid as their appearance as figure is more conspicuous. Therefore the spatial perception does not seem to depend on adaptation or associative learning. The essential factor is indeed phenomenological. Neither is spatial perception a matter of cognizing the sensations according to an interpretation in connection with which the appearances end up being thoroughly adjusted, so that it would be impossible to decide the equivalence between figures in spaces with different properties unless on the grounds of a stipulative defini­tion. Nor is it somehow bound to satisfy the Euclidean properties of space, so that illusions or errors of judgement should always occur, which would have to be tolerated were the adjustment not fully realized.

As an indirect demonstration, Gerhards combines two configurations by testing the perceptual property of being a figure against the functional role of figure and ground. He changes Gj into the Euclidean figure G** by making the Euclidean distance from P_i to P equal, thus providing it with Euclidean rigid­ity. Next he presents G** at rest over G₃, which is the non-Euclidean configura­tion with the strongest figure characterization, which is instead set in quasi­rotation. G₃ appears still rigid, while G** appears to be deformed in the opposite direction of the distortions that are drawn in G₃ but yet not perceived. The left external point of G** appears nearer to P than the right one, and at the same time G** stands out as a flat and frontal-parallel figure on the conic ground G₃. If even G** is set in quasi-rotation and overtakes G₃, the external points of G** move toward and away from P as they pass from the right to the left side of G₃ and vice versa. This deformation of G** remains visible even if the fulcrum P of G₃ is drawn to be placed even farther from the middle of E on the right, making the drawing of G₃ so distorted that it no longer appears rigid. The deforma­tion of G** disappears if G** is also drawn with the same distortions of G₃, for example by shortening the distance from the external points on the right to P while lengthening that from the external points on the left. This configuration is similar to Gj but now not only does it appear rigid, the distances from the external points P_i to P also appear equal. Gerhards emphasizes that this ap­pearance is obtained through a deformation of G** that is considerably smaller than that of G₃.

Gerhards concludes that perceptual rigidity is the result of the competition between configurations for their spatial properties, together with the space to which they belong, to emerge. The more conspicuous the figure characteriza­tion of a configuration, the more it succeeds in imposing a space as a system of reference. However, the configurations that do not win still have an effect. This effect is manifest in the Euclidean deformations that are not thoroughly resolved into the rigidity of the Lobachevsky figures and in the ever decreasing appearances of deformations from the Euclidean standpoint in G₁, G₂ and G₃, in which they occur the least.

As regards the general question about visual judgements on body proper­ties in different spaces, one may conclude that the spatial perception within a model cannot be described as the result of the simple replacement of the Euclidean by the Lobachevsky interpretation of sensations. As regards the ap­pearances of the space given the model of which the perceptual standpoint is part, the last experiment shows that even the ground along with the configura­tion induces a spatial system of reference. For this reason G** presents the op­posite deformations in relation to those in the drawing of G₃, while it presents none if the same distortions are drawn on it. One may infer that G₁ appears to be deformed, although it is a rigid body in the Lobachevsky space, because it has no Euclidean ground against which to compete and not because of a Eu­clidean habit from which perception is deemed able to wean itself.

This account gives the ideal construct of mapping an interpretation in the phenomenological theory. If the empty ground behaves as a Euclidean sys­tem of reference, one may infer that the Euclidean space may be, as it were, a privileged system of reference. On the one hand, this accounts for the obser­vation that the visual paradox from the Euclidean standpoint is strengthened as the configurations appear more and more as figures of non-Euclidean rigid bodies. On the other hand, it allows for Euclidean models of non-Euclidean spaces intended as spatial systems of reference built from suitable perceivable properties.

Source: Calì Carmelo (2017), Phenomenology of Perception: Theories and Experimental Evidence, Brill.