Vegetron’s chief financial officer (CFO) is wondering how to analyze a proposed $1 million investment in a new venture code-named project X. He asks what you think.
Your response should be as follows: “First, forecast the cash flows generated by project X over its economic life. Second, determine the appropriate opportunity cost of capital (r). This should reflect both the time value of money and the risk involved in project X. Third, use this opportunity cost of capital to discount the project’s future cash flows. The sum of the discounted cash flows is called present value (PV). Fourth, calculate net present value (NPV) by subtracting the $1 million investment from PV. If we call the cash flows C0, C1, and so on, then
![]()
where C0 = -$1 million. We should invest in project X if its NPV is greater than zero.”
However, Vegetron’s CFO is unmoved by your sagacity. He asks why NPV is so important.
You: Let us look at what is best for Vegetron stockholders. They want you to make their Veg- etron shares as valuable as possible.
Right now Vegetron’s total market value (price per share times the number of shares outstanding) is $10 million. That includes $1 million cash, which we can invest in project X. The value of Vegetron’s other assets and opportunities must therefore be $9 million. We have to decide whether it is better to keep the $1 million cash and reject project X or to spend the cash and accept the project. Let us call the value of the new project PV. Then the choice is as follows:
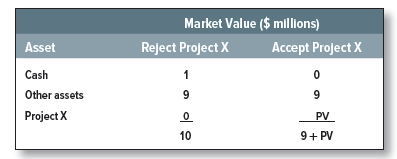
Clearly project X is worthwhile if its present value (PV) is greater than $1 million, that is, if net present value is positive.
CFO: How do I know that the PV of project X will actually show up in Vegetron’s market value?
You: Suppose we set up a new, independent firm X, whose only asset is project X. What would be the market value of firm X?
Investors would forecast the dividends that firm X would pay and discount those dividends by the expected rate of return of securities having similar risks. We know that stock prices are equal to the present value of forecasted dividends.
Since project X is the only asset, the dividend payments we would expect firm X to pay are exactly the cash flows we have forecasted for project X. Moreover, the rate that investors would use to discount firm X’s dividends is exactly the rate we should use to discount project X’s cash flows.
I agree that firm X is hypothetical. But if project X is accepted, investors holding Vegetron stock will really hold a portfolio of project X and the firm’s other assets. We know the other assets are worth $9 million considered as a separate venture. Since asset values add up, we can easily figure out the portfolio value once we calculate the value of project X as a separate venture.
By calculating the present value of project X, we are replicating the process by which the common stock of firm X would be valued in the financial markets.
CFO: The one thing I don’t understand is where the discount rate comes from.
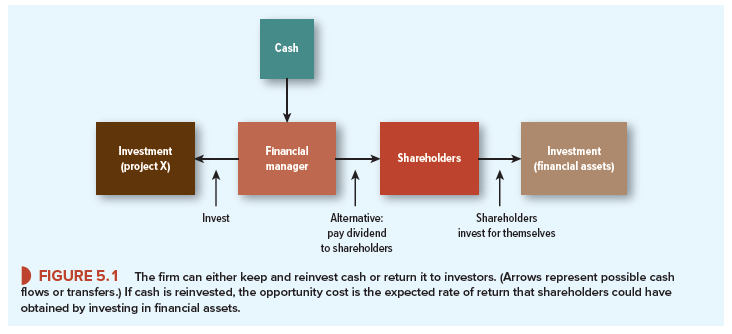
You: I agree that the discount rate is difficult to measure precisely. But it is easy to see what we are trying to measure. The discount rate is the opportunity cost of investing in the project rather than in the financial markets. In other words, instead of accepting a project, the firm can always return the cash to the shareholders and let them invest it in financial assets.
You can see the trade-off (Figure 5.1). The opportunity cost of taking the project is the return shareholders could have earned had they invested the money on their own. When we discount the project’s cash flows by the expected rate of return on financial assets, we are measuring how much investors would be prepared to pay for your project.
CFO: But which financial assets? The fact that investors expect only 12% on IBM stock does not mean that we should purchase Fly-by-Night Electronics if it offers 13%.
You: The opportunity-cost concept makes sense only if assets of equivalent risk are compared. In general, you should identify financial assets that have the same risk as your project, estimate the expected rate of return on these assets, and use this rate as the opportunity cost.
1. Net Present Value’s Competitors
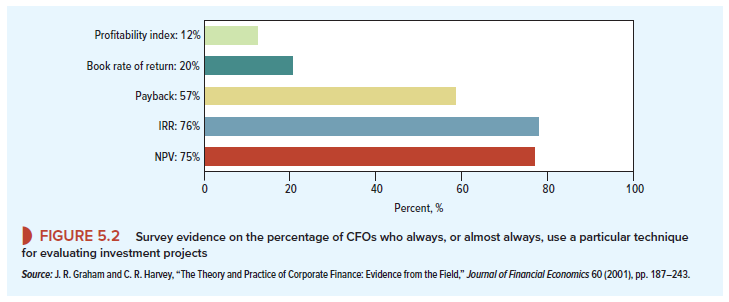
When you advised the CFO to calculate the project’s NPV, you were in good company. These days, 75% of firms always, or almost always, calculate net present value when deciding on investment projects. However, as you can see from Figure 5.2, NPV is not the only investment criterion that companies use, and firms often look at more than one measure of a project’s attractiveness.
About three-quarters of firms calculate the project’s internal rate of return (or IRR); that is roughly the same proportion as use NPV. The IRR rule is a close relative of NPV and, when used properly, it will give the same answer. You therefore need to understand the IRR rule and how to take care when using it.
A large part of this chapter is concerned with explaining the IRR rule, but first we look at two other measures of a project’s attractiveness—the project’s payback and its book rate of return. As we will explain, both measures have obvious defects. Few companies rely on them to make their investment decisions, but they do use them as supplementary measures that may help to distinguish the marginal project from the no-brainer.
Later in the chapter we also come across one further investment measure, the profitability index. Figure 5.2 shows that it is not often used, but you will find that there are circumstances in which this measure has some special advantages.
2. Three Points to Remember about NPV
As we look at these alternative criteria, it is worth keeping in mind the following key features of the net present value rule. First, the NPV rule recognizes that a dollar today is worth more than a dollar tomorrow because the dollar today can be invested to start earning interest immediately. Any investment rule that does not recognize the time value of money cannot be sensible. Second, net present value depends solely on the forecasted cash flows from the project and the opportunity cost of capital. Any investment rule that is affected by the manager’s tastes, the company’s choice of accounting method, the profitability of the company’s existing business, or the profitability of other independent projects will lead to inferior decisions. Third, because present values are all measured in today’s dollars, you can add them up. Therefore, if you have two projects A and B, the net present value of the combined investment is
NPV(A + B) = NPV(A) + NPV(B)
This adding-up property has important implications. Suppose project B has a negative NPV. If you tack it onto project A, the joint project (A + B) must have a lower NPV than A on its own. Therefore, you are unlikely to be misled into accepting a poor project (B) just because it is packaged with a good one (A). As we shall see, the alternative measures do not have this property. If you are not careful, you may be tricked into deciding that a package of a good and a bad project is better than the good project on its own.

24 Jun 2021
25 Jun 2021
25 Jun 2021
24 Jun 2021
23 Jun 2021
24 Jun 2021