Determining the Sample Size

In providing practical advice in the two preceding sections, we commented on the role of the sample size in providing good approximate confidence intervals when the population is not normally distributed. In this section, we focus on another aspect of the sample size issue. We describe how to choose a sample size large enough to provide a desired margin of error. To understand how this process works, we return to the s known case presented in Section 8.1. Using expression (8.1), the interval estimate is

The quantity z_a/2(σ/√n) is the margin of error. Thus, we see that z_a/2, the population stand­ard deviation s, and the sample size n combine to determine the margin of error. Once we select a confidence coefficient 1 – a, z_a/2 can be determined. Then, if we have a value for s, we can determine the sample size n needed to provide any desired margin of error. Development of the formula used to compute the required sample size n follows.

Let E = the desired margin of error:

Squaring both sides of this equation, we obtain the following expression for the sample size.

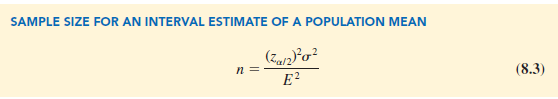
This sample size provides the desired margin of error at the chosen confidence level.

In equation (8.3), E is the margin of error that the user is willing to accept, and the value of z_a/2 follows directly from the confidence level to be used in developing the interval estimate. Although user preference must be considered, 95% confidence is the most fre­quently chosen value (z.₀₂₅ = 1.96).

Finally, use of equation (8.3) requires a value for the population standard deviation s. However, even if s is unknown, we can use equation (8.3) provided we have a preliminary or planning value for s. In practice, one of the following procedures can be chosen.

1. Use the estimate of the population standard deviation computed from data of previ­ous studies as the planning value for s.
2. Use a pilot study to select a preliminary sample. The sample standard deviation from the preliminary sample can be used as the planning value for s.
3. Use judgment or a “best guess” for the value of s. For example, we might begin by estimating the largest and smallest data values in the population. The difference between the largest and smallest values provides an estimate of the range for the data. Finally, the range divided by 4 is often suggested as a rough approximation of the standard deviation and thus an acceptable planning value for s.

Let us demonstrate the use of equation (8.3) to determine the sample size by considering the following example. A previous study that investigated the cost of renting automobiles in the United States found a mean cost of approximately $55 per day for renting a midsize automobile. Suppose that the organization that conducted this study would like to conduct a new study in order to estimate the population mean daily rental cost for a midsize auto­mobile in the United States. In designing the new study, the project director specifies that the population mean daily rental cost be estimated with a margin of error of $2 and a 95% level of confidence.

The project director specified a desired margin of error of E = 2, and the 95% level of confidence indicates z.₀₂₅ = 1.96. Thus, we only need a planning value for the population standard deviation s in order to compute the required sample size. At this point, an analyst reviewed the sample data from the previous study and found that the sample standard deviation for the daily rental cost was $9.65. Using 9.65 as the planning value for s, we obtain

Thus, the sample size for the new study needs to be at least 89.43 midsize automobile rentals in order to satisfy the project director’s $2 margin-of-error requirement. In cases where the computed n is not an integer, we round up to the next integer value; hence, the recommended sample size is 90 midsize automobile rentals.

Source:  Anderson David R., Sweeney Dennis J., Williams Thomas A. (2019), Statistics for Business & Economics, Cengage Learning; 14th edition.