Equity and Efficiency

We have shown that different efficient allocations of goods are possible, and we have seen how a perfectly competitive economy generates a Pareto efficient allocation. But there are many Pareto efficient allocations, and some are likely to be more fair than others. How do we decide what is the most equitable alloca- tion? That is a difficult question—economists and others disagree both about how to define equity and how to quantify it. Any such view would involve sub- jective comparisons of utility, and reasonable people could disagree about how to make these comparisons. In this section, we discuss this general point and then illustrate it in a particular case by showing that there is no reason to believe that the allocation associated with a competitive equilibrium will be equitable.

1. The Utility Possibilities Frontier

Recall that every point on the contract curve in our two-person exchange economy shows the levels of utility that James and Karen can achieve. In Figure 16.8 we put the information from the Edgeworth box in a different form. James’s utility is mea- sured on the horizontal axis and Karen’s on the vertical axis. Every point in the Edgeworth box corresponds to a point in Figure 16.7 because every allocation gen- erates utility for both people. Every movement to the right in Figure 16.8 represents an increase in James’s utility, and every upward movement an increase in Karen’s.

The utility possibilities frontier represents all allocations that are Pareto efficient. It shows the levels of satisfaction that are achieved when the two individuals have reached the contract curve. Point OJ  is one extreme at which James has no goods and therefore zero utility, while point OK  is the opposite extreme at which Karen has no goods. Because all other points on the frontier, such as E, F, and G, corre- spond to points on the contract curve, one person cannot be made better off with- out making the other worse off. Point H, however, represents an inefficient alloca- tion because any trade within the shaded area makes one or both parties better off. At L, both people would be better off, but L is not attainable because there is not enough of both goods to generate the levels of utility that the point represents.

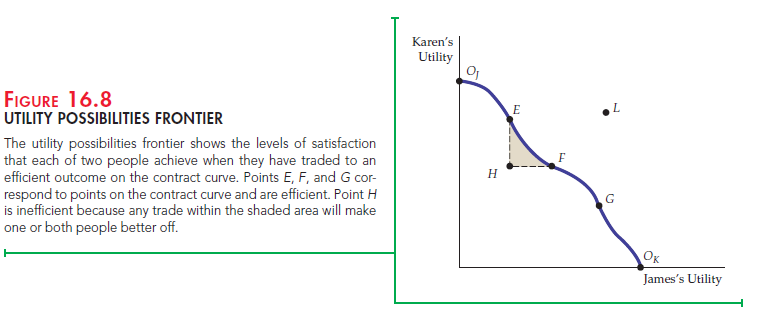
It might seem reasonable to conclude that an allocation must be Pareto effi- cient to be equitable. Compare point H with F and E. Both F and E are efficient, and (relative to H) each makes one person better off without making the other worse off. We might agree, therefore, that it is inequitable to James or Karen or both for an economy to yield allocation H as opposed to F or E.

But suppose H and G are the only possible allocations. Is G more equitable than H? Not necessarily. Compared with H, G yields more utility for James and less for Karen. Some people may feel that G is more equitable than H; others may feel the opposite. We can conclude, therefore, that one Pareto inefficient allo- cation of resources may be more equitable than another Pareto efficient allocation.

The problem is how to define an equitable allocation. Even if we restrict our- selves to all points on the utility possibilities frontier, we can still ask which of these points is the most equitable. The answer depends on what one thinks equity entails and, therefore, on the interpersonal comparisons of utility that one is willing to make.

SOCIAL WELFARE FUNCTIONS In economics, we often use a social welfare function to describe the well-being of society as a whole in terms of utilities of individual members. A social welfare function is useful when we want to evalu- ate policies that affect some members of society differently than others.

One such function, the utilitarian, weights everyone’s utility equally and consequently maximizes the total utility of all members of society. Each social welfare function can be associated with a particular view about equity. But some views do not explicitly weight individual utilities and cannot therefore be represented by a social welfare function. For example, a market-oriented view argues that the outcome of the competitive market process is equitable because it rewards those who are most able and who work the hardest. If E is the com- petitive equilibrium allocation, for example, E would be deemed to be more equitable than F, even though goods are less equally allocated.

When more than two people are involved, the meaning of the word equity becomes even more complex. The Rawlsian view3  considers a world in which people do not know in advance what their individual endowments will be. Rawls argues that, faced with a world in which you do not know your own “fate,” you would opt for a system ensuring that the least well-off person in society will be treated reasonably well. Specifically, according to Rawls, the most equitable allocation maximizes the utility of the least-well-off person in society. The Rawlsian perspective could be egalitarian—involving an equal allocation of goods among all members of society. But it need not be. Suppose that by rewarding more productive people more highly than less productive people, we can get the most productive people to work harder. This policy could produce more goods and services, some of which could then be reallocated to make the poorest members of society better off.

The four views of equity in Table 16.2 move roughly from most to least egalitarian. While the egalitarian view explicitly requires equal allocations, the Rawlsian puts a heavy weight on equality (otherwise, some people would be much worse off than others). The utilitarian is likely to require some difference between the best- and worst-off members of society. Finally, the market-oriented view may lead to substantial inequality in the allocations of goods and services.

2. Equity and Perfect Competition

A competitive equilibrium leads to a Pareto efficient outcome that may or may not be equitable. In fact, a competitive equilibrium could occur at any point on the con­tract curve, depending on the initial allocation. Imagine, for example, that the initial allocation gave all food and clothing to Karen. This would be at Oj in Figure 16.8, and Karen would have no reason to trade. Point O_j would then be a competitive equilibrium, as would point O_k and all intermediate points on the contract curve.

Because efficient allocations are not necessarily equitable, society must rely to some extent on government to achieve equity goals by redistributing income or goods among households. These goals can be reached through the tax system. For example, a progressive income tax whose funds are used for programs that benefit households proportionally to income will redistribute income from the wealthy to the poor. The government can also provide public services, such as medical aid to the poor (Medicaid), or it can transfer funds through such pro­grams as food stamps.

The result that a competitive equilibrium can sustain every point on the con­tract curve is a fundamental result in microeconomics. It is important because it suggests an answer to a basic normative question: Is there a trade-off between equity and efficiency? In other words, must a society that wishes to achieve a more equitable allocation of resources necessarily operate in a manner that
is Pareto efficient? The answer, which is given by the second theorem of welfare economics, tells us that redistribution need not conflict with economic efficiency.

Formally, the second theorem states the following:

Literally, this theorem tells us that any equilibrium deemed to be equitable can be achieved by a suitable distribution of resources among individuals and that such a distribution need not in itself generate inefficiencies. Unfortunately, all programs that redistribute income in our society are economically costly. Taxes may encourage individuals to work less or cause firms to devote resources to avoiding taxes rather than to producing output. So, in effect, there is a trade-off between the goals of equity and efficiency, and hard choices must be made. Welfare economics, which builds on the first and second theorems, provides a useful framework for debating the normative issues that surround the equity– efficiency issue in public policy.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.