Introduction to Sampling Distributions

In the preceding section we said that the sample mean X is the point estimator of the population mean m, and the sample proportion p is the point estimator of the population proportion p. For the simple random sample of 30 EAI managers shown in Table 7.2, the point estimate of m is X = $71,814 and the point estimate of p is p = .63. Suppose we select another simple random sample of 30 EAI managers and obtain the following point estimates:

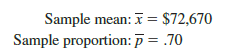
Note that different values of X and p were obtained. Indeed, a second simple random sample of 30 EAI managers cannot be expected to provide the same point estimates as the first sample.

Now, suppose we repeat the process of selecting a simple random sample of 30 EAI managers over and over again, each time computing the values of X and p. Table 7.4 con­tains a portion of the results obtained for 500 simple random samples, and Table 7.5 shows the frequency and relative frequency distributions for the 500 X values. Figure 7.1 shows the relative frequency histogram for the X values.

In Chapter 5 we defined a random variable as a numerical description of the outcome of an experiment. If we consider the process of selecting a simple random sample as an experiment, the sample mean X is the numerical description of the outcome of the experiment. Thus, the sample mean X is a random variable. As a result, just like other random variables, X has a mean or expected value, a standard deviation, and a probability distribution. Because the various possible values of X are the result of different simple random samples, the probability distribution of X is called the sampling distribution of X. Knowledge of this sampling distribution and its properties will enable us to make probability statements about how close the sample mean X is to the population mean m.

Let us return to Figure 7.1. We would need to enumerate every possible sample of 30 managers and compute each sample mean to completely determine the sampling distribution of X. However, the histogram of 500 X values gives an approximation of this sampling distribution. From the approximation we observe the bell-shaped appearance of the distribution. We note that the largest concentration of the X values and the mean of the 500 X values are near the population mean m = $71,800. We will describe the properties of the sampling distribution of X more fully in the next section.

The 500 values of the sample proportion p are summarized by the relative frequency histogram in Figure 7.2. As in the case of X, p is a random variable. If every possible sample of size 30 were selected from the population and if a value of p were computed for each sample, the resulting probability distribution would be the sampling distribution of p. The relative frequency histogram of the 500 sample values in Figure 7.2 provides a general idea of the appearance of the sampling distribution of p.

In practice, we select only one simple random sample from the population. We repeated the sampling process 500 times in this section simply to illustrate that many different samples are possible and that the different samples generate a variety of values for the sample statistics X and p. The probability distribution of any particular sample statistic is called the sampling distribution of the statistic. In Section 7.5 we show the characteristics of the sampling distribution of X. In Section 7.6 we show the characteristics of the sampling distribution of p.

Source:  Anderson David R., Sweeney Dennis J., Williams Thomas A. (2019), Statistics for Business & Economics, Cengage Learning; 14th edition.