Marginal Revenue, Marginal Cost, and Profit Maximization

We now return to our working assumption of profit maximization and examine the implications of this objective for the operation of a firm. We will begin by looking at the profit-maximizing output decision for any firm, whether it operates in a perfectly competitive market or is one that can influence price. Because profit is the difference between (total) revenue and (total) cost, finding the firm’s profit-maximizing output level means analyzing its revenue. Suppose that the firm’s output is q, and that it obtains revenue R. This revenue is equal to the price of the product P times the number of units sold: R = Pq. The cost of production C also depends on the level of output. The firm’s profit, p, is the difference between revenue and cost:

(Here we show explicitly that p, R, and C depend on output. Usually we will omit this reminder.)
To maximize profit, the firm selects the output for which the difference between revenue and cost is the greatest. This principle is illustrated in Figure 8.1. Revenue R(q) is a curved line, which reflects the fact that the firm can sell a greater level of output only by lowering its price. The slope of this revenue curve is marginal revenue: the change in revenue resulting from one unit
increase in output.

Also shown is the total cost curve C(q). The slope of this curve, which measures the additional cost of producing one additional unit of output, is the firm’s marginal cost. Note that total cost C(q) is positive when output is zero because there is a fixed cost in the short run.

For the firm illustrated in Figure 8.1, profit is negative at low levels of out­put because revenue is insufficient to cover fixed and variable costs. As output increases, revenue rises more rapidly than cost, so that profit eventually becomes positive. Profit continues to increase until output reaches the level q*. At this point, marginal revenue and marginal cost are equal, and the vertical distance between revenue and cost, AB, is greatest. q* is the profit-maximizing output level. Note that at output levels above q*, cost rises more rapidly than revenue— i.e., marginal revenue is less than marginal cost. Thus, profit declines from its maximum when output increases above q*.

The rule that profit is maximized when marginal revenue is equal to marginal cost holds for all firms, whether competitive or not. This important rule can also be derived algebraically. Profit, p = R — C, is maximized at the point at which an additional increment to output leaves profit unchanged (i.e., Ap/ Aq = 0):

AR/ Aq is marginal revenue MR and AC/ Aq is marginal cost MC. Thus we con­clude that profit is maximized when MR — MC = 0, so that

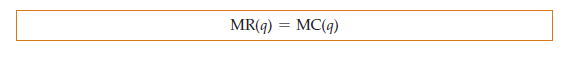
1. Demand and Marginal Revenue for a Competitive Firm

Because each firm in a competitive industry sells only a small fraction of the entire industry output, how much output the firm decides to sell will have no effect on the market price of the product. The market price is determined by the industry demand and supply curves. Therefore, the competitive firm is a price taker. Recall that price taking is one of the fundamental assumptions of perfect competition. The price-taking firm knows that its production decision will have no effect on the price of the product. For example, when a farmer is deciding how many acres of wheat to plant in a given year, he can take the market price of wheat—say, $4 per bushel—as given. That price will not be affected by his acreage decision.

Often we will want to distinguish between market demand curves and the demand curves faced by individual firms. In this chapter we will denote mar- ket output and demand by capital letters (Q and D) and the firm’s output and demand by lowercase letters (q and d).

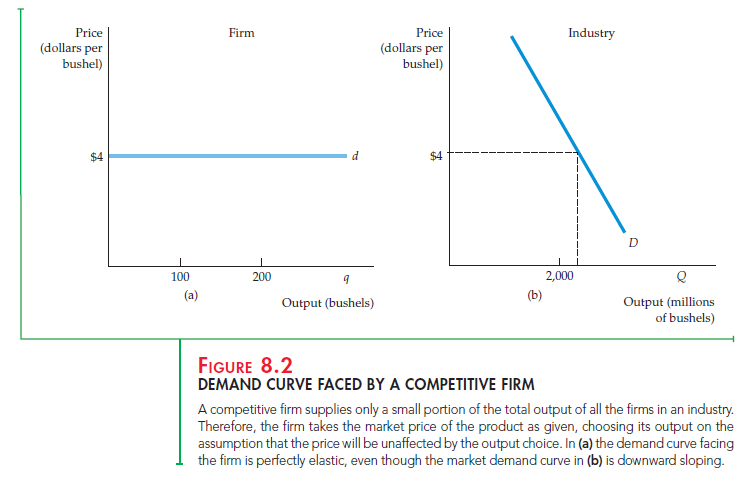
Because it is a price taker, the demand curve d facing an individual competitive firm is given by a horizontal line. In Figure 8.2(a), the farmer ’s demand curve cor- responds to a price of $4 per bushel of wheat. The horizontal axis measures the amount of wheat that the farmer can sell, and the vertical axis measures the price.

Compare the demand curve facing the firm (in this case, the farmer) in Figure 8.2(a) with the market demand curve D in Figure 8.2(b). The market demand curve shows how much wheat all consumers will buy at each possible price. It is downward sloping because consumers buy more wheat at a lower price. The demand curve facing the firm, however, is horizontal because the firm’s sales will have no effect on price. Suppose the firm increased its sales from 100 to 200 bushels of wheat. This would have almost no effect on the mar- ket because industry output is 2,000 million bushels. Price is determined by the interaction of all firms and consumers in the market, not by the output decision of a single firm.

By the same token, when an individual firm faces a horizontal demand curve, it can sell an additional unit of output without lowering price. As a result, when it sells an additional unit, the firm’s total revenue increases by an amount equal to the price: one bushel of wheat sold for $4 yields additional revenue of $4. Thus, marginal revenue is constant at $4. At the same time, average revenue received by

the firm is also $4 because every bushel of wheat produced will be sold at $4.

Therefore:

2. Profit Maximization by a Competitive Firm

Because the demand curve facing a competitive firm is horizontal, so that MR = P, the general rule for profit maximization that applies to any firm can be simplified. A perfectly competitive firm should choose its output so that marginal cost equals price:

Note that because competitive firms take price as fixed, this is a rule for setting output, not price.

The choice of the profit-maximizing output by a competitive firm is so impor­tant that we will devote most of the rest of this chapter to analyzing it. We begin with the short-run output decision and then move to the long run.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.