Present Value Concepts and Pricing Bonds Payable

When a corporation issues bonds, the price that investors are willing to pay for the bonds depends on the following:

1. The face amount of the bonds, which is the amount due at the maturity date.
2. The periodic interest to be paid on the bonds.
3. The market rate of interest.

An investor determines how much to pay for the bonds by computing the present value of the bond’s future cash receipts, using the market rate of interest. A bond’s future cash receipts include its face value at maturity and the periodic interest payments.

1. Present Value Concepts

The concept of present value is based on the time value of money. The time value of money concept recognizes that cash received today is worth more than the same amount of cash to be received in the future.

To illustrate, what would you rather have: $1,000 today or $1,000 one year from now? You would rather have the $1,000 today because it could be invested to earn interest. For example, if the $1,000 could be invested to earn 10% per year, the $1,000 will accumulate to $1,100 ($1,000 plus $100 interest) in one year. In this sense, you can think of the $1,000 in hand today as the present value of $1,100 to be received a year from today. This present value is illustrated below.

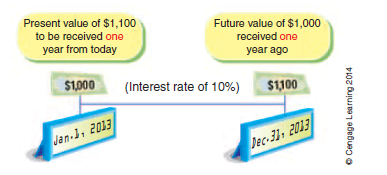
A related concept to present value is future value. To illustrate, using the preceding example, the $1,100 to be received on December 31, 2013, is the future value of $1,000 on January 1, 2013, assuming an interest rate of 10%.

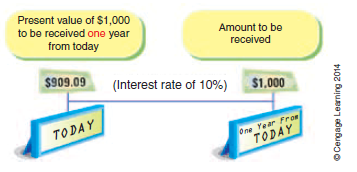
Present Value of an Amount To illustrate the present value of an amount, assume that $1,000 is to be received in one year. If the market rate of interest is 10%, the present value of the $1,000 is $909.09 ($1,000/1.10). This present value is illustrated below.

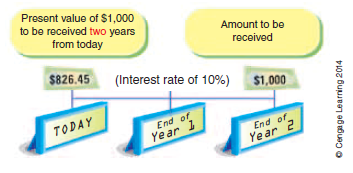
If the $1,000 is to be received in two years, with interest of 10% compounded at the end of the first year, the present value is $826.45 ($909.09/1.10).6 This present value is illustrated below.

The present value of an amount to be received in the future can be determined by a series of divisions such as illustrated on the previous page. In practice, however, it is easier to use a table of present values.

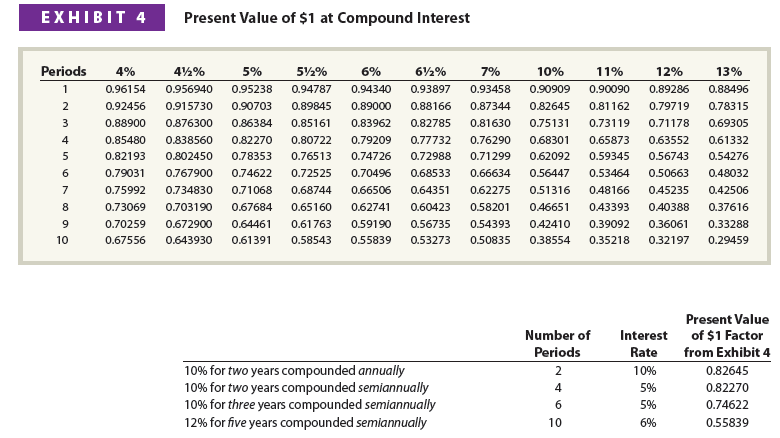
The present value of $1 table is used to find the present value factor for $1 to be received after a number of periods in the future. The amount to be received is then multiplied by this factor to determine its present value.

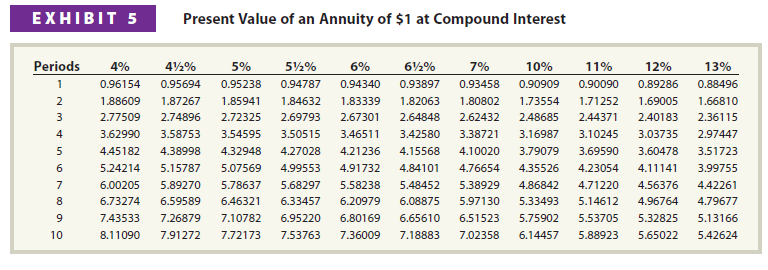
To illustrate, Exhibit 4 is a partial table of the present value of $1.^[1] Exhibit 4 indicates that the present value of $1 to be received in two years with a market rate of interest of 10% a year is 0.82645. Multiplying $1,000 to be received in two years by 0.82645 yields $826.45 ($1,000 x 0.82645). This amount is the same amount computed earlier. In Exhibit 4, the Periods column represents the number of com­pounding periods, and the percentage columns represent the compound interest rate per period. Thus, the present value factor from Exhibit 4 for 12% for five years is 0.56743 If the interest is compounded semiannually, the interest rate is 6% (12% divided by 2), and the number of periods is 10 (5 years x 2 times per year). Thus, the present value factor from Exhibit 4 for 6% and 10 periods is 0.55839.

Some additional examples using Exhibit 4 are shown below.

Present value of the Periodic Receipts A series of equal cash receipts spaced equally in time is called an annuity. The present value of an annuity is the sum of the present values of each cash receipt. To illustrate, assume that $100 is to be received annually for two years and that the market rate of interest is 10%. Using Exhibit 4, the present value of the receipt of the two amounts of $100 is $173.55, as shown on the next page.

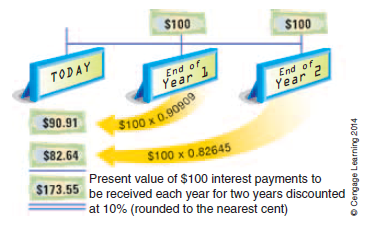
Instead of using present value of $1 tables to determine the present value of each cash flow separately, such as Exhibit 4, the present value of an annuity can be com­puted in a single step. Using a value from the present value of an annuity of $1 table in Exhibit 5, the present value of the entire annuity can be calculated by multiplying the equal cash payment times the appropriate present value of an annuity of $1.

To illustrate, the present value of $100 to be received at the end of each of the next two years at 10% compound interest per period is $173.55 ($100 x 1.73554). This amount is the same amount computed above using the present value of $1.

2. Pricing Bonds

The selling price of a bond is the sum of the present values of:

1. The face amount of the bonds due at the maturity date
2. The periodic interest to be paid on the bonds

The market rate of interest is used to compute the present value of both the face amount and the periodic interest.

To illustrate the pricing of bonds, assume that Southern Utah Communications Inc. issued the following bond on January 1, 2013:

Market Rate of Interest of 12% Assuming bonds would sell for their face amount. As shown by the following present value computa­tions, the bonds would sell for $100,000.

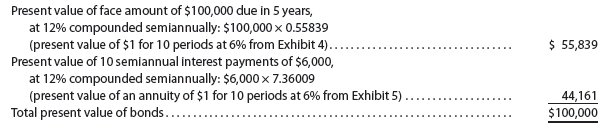
Market Rate of Interest of 13% Assuming bonds would sell at a discount. As shown by the following present value computations, the bonds would sell for $96,406.⁸

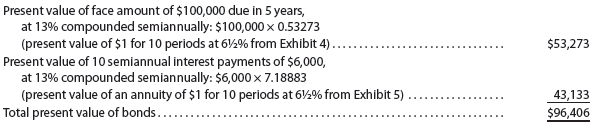
Market Rate of Interest of 11% Assuming a market rate of interest of 11%, the bonds would sell at a premium. As shown by the following present value computations, the bonds would sell for $103,769.

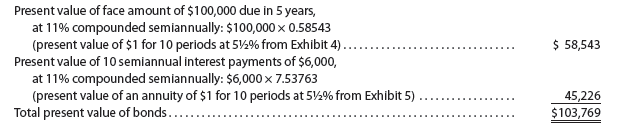
As shown above, the selling price of the bond varies with the present value of the bond’s face amount at maturity, interest payments, and the market rate of interest.

Source: Warren Carl S., Reeve James M., Duchac Jonathan (2013), Corporate Financial Accounting, South-Western College Pub; 12th edition.