As the recent growth in state lotteries shows, people sometimes choose risky alternatives that suggest risk-loving rather than risk-averse behavior. Most people, however, spend relatively small amounts on lottery tickets and casinos. When more important decisions are involved, they are generally risk averse. In this section, we describe three ways by which both consumers and businesses commonly reduce risks: diversification, insurance, and obtaining more information about choices and payoffs.
1. Diversification
Recall the old saying, “Don’t put all your eggs in one basket.” Ignoring this advice is unnecessarily risky: If your basket turns out to be a bad bet, all will be lost. Instead, you can reduce risk through diversification: allocating your resources to a variety of activities whose outcomes are not closely related.
Suppose, for example, that you plan to take a part-time job selling appliances on a commission basis. You can decide to sell only air conditioners or only heat- ers, or you can spend half your time selling each. Of course, you can’t be sure how hot or cold the weather will be next year. How should you apportion your time in order to minimize the risk involved?
Risk can be minimized by diversification—by allocating your time so that you sell two or more products (whose sales are not closely related) rather than a
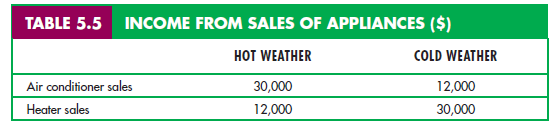
single product. Suppose there is a 0.5 probability that it will be a relatively hot year, and a 0.5 probability that it will be cold. Table 5.5 gives the earnings that you can make selling air conditioners and heaters.
If you sell only air conditioners or only heaters, your actual income will be either $12,000 or $30,000, but your expected income will be $21,000 (.5[$30,000]
+ .5[$12,000]). But suppose you diversify by dividing your time evenly between the two products. In that case, your income will certainly be $21,000, regardless of the weather. If the weather is hot, you will earn $15,000 from air conditioner sales and $6000 from heater sales; if it is cold, you will earn $6000 from air con- ditioners and $15,000 from heaters. In this instance, diversification eliminates all risk.
Of course, diversification is not always this easy. In our example, heater and air conditioner sales are negatively correlated variables—they tend to move in opposite directions; whenever sales of one are strong, sales of the other are weak. But the principle of diversification is a general one: As long as you can allocate your resources toward a variety of activities whose outcomes are not closely related, you can eliminate some risk.
THE STOCK MARKET Diversification is especially important for people who invest in the stock market. On any given day, the price of an individual stock can go up or down by a large amount, but some stocks rise in price while oth- ers fall. An individual who invests all her money in a single stock (i.e., puts all her eggs in one basket) is therefore taking much more risk than necessary. Risk can be reduced—although not eliminated—by investing in a portfolio of ten or twenty different stocks. Likewise, you can diversify by buying shares in mutual funds: organizations that pool funds of individual investors to buy a large num- ber of different stocks. There are thousands of mutual funds available today for both stocks and bonds. These funds are popular because they reduce risk through diversification and because their fees are typically much lower than the cost of assembling one’s own portfolio of stocks.
In the case of the stock market, not all risk is diversifiable. Although some stocks go up in price when others go down, stock prices are to some extent positively correlated variables: They tend to move in the same direction in response to changes in economic conditions. For example, the onset of a severe recession, which is likely to reduce the profits of many companies, may be accompanied by a decline in the overall market. Even with a diversified portfo- lio of stocks, therefore, you still face some risk.
2. Insurance
We have seen that risk-averse people are willing to pay to avoid risk. In fact, if the cost of insurance is equal to the expected loss (e.g., a policy with an expected loss of $1000 will cost $1000), risk-averse people will buy enough insurance to recover fully from any financial losses they might suffer.
Why? The answer is implicit in our discussion of risk aversion. Buying insur- ance assures a person of having the same income whether or not there is a loss. Because the insurance cost is equal to the expected loss, this certain income is equal to the expected income from the risky situation. For a risk-averse con- sumer, the guarantee of the same income regardless of the outcome generates more utility than would be the case if that person had a high income when there was no loss and a low income when a loss occurred.
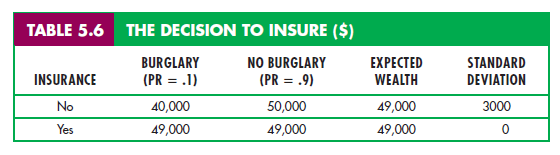
To clarify this point, let’s suppose a homeowner faces a 10-percent probabil- ity that his house will be burglarized and he will suffer a $10,000 loss. Let’s assume he has $50,000 worth of property. Table 5.6 shows his wealth in two situ- ations—with insurance costing $1000 and without insurance.
Note that expected wealth is the same ($49,000) in both situations. The vari- ability, however, is quite different. As the table shows, with no insurance the standard deviation of wealth is $3000; with insurance, it is 0. If there is no burglary, the uninsured homeowner gains $1000 relative to the insured hom- eowner. But with a burglary, the uninsured homeowner loses $9000 relative to the insured homeowner. Remember: for a risk-averse individual, losses count more (in terms of changes in utility) than gains. A risk-averse homeowner, there- fore, will enjoy higher utility by purchasing insurance.
THE LAW OF LARGE NUMBERS Consumers usually buy insurance from companies that specialize in selling it. Insurance companies are firms that offer insurance because they know that when they sell a large number of poli- cies, they face relatively little risk. The ability to avoid risk by operating on a large scale is based on the law of large numbers, which tells us that although single events may be random and largely unpredictable, the average outcome of many similar events can be predicted. For example, I may not be able to predict whether a coin toss will come out heads or tails, but I know that when many coins are flipped, approximately half will turn up heads and half tails. Likewise, if I am selling automobile insurance, I cannot predict whether a particular driver will have an accident, but I can be reasonably sure, judg- ing from past experience, what fraction of a large group of drivers will have accidents.
ACTUARIAL FAIRNESS By operating on a large scale, insurance companies can be sure that over a sufficiently large number of events, total premiums paid in will be equal to the total amount of money paid out. Let’s return to our burglary example. A man knows that there is a 10-percent probability that his house will be burgled; if it is, he will suffer a $10,000 loss. Prior to facing this risk, he calculates the expected loss to be $1000 (.10 X $10,000). The risk involved is considerable, however, because there is a 10-percent probability of
a large loss. Now suppose that 100 people are similarly situated and that all of them buy burglary insurance from the same company. Because they all face a
10-percent probability of a $10,000 loss, the insurance company might charge each of them a premium of $1000. This $1000 premium generates an insurance fund of $100,000 from which losses can be paid. The insurance company can rely on the law of large numbers, which holds that the expected loss to the 100 individuals as a whole is likely to be very close to $1000 each. The total payout, therefore, will be close to $100,000, and the company need not worry about los- ing more than that.
When the insurance premium is equal to the expected payout, as in the exam- ple above, we say that the insurance is actuarially fair. But because they must cover administrative costs and make some profit, insurance companies typi- cally charge premiums above expected losses. If there are a sufficient number of insurance companies to make the market competitive, these premiums will be close to actuarially fair levels. In some states, however, insurance premiums are regulated in order to protect consumers from “excessive” premiums. We will examine government regulation of markets in detail in Chapters 9 and 10 of this book.
In recent years, some insurance companies have come to the view that cat- astrophic disasters such as earthquakes are so unique and unpredictable that they cannot be viewed as diversifiable risks. Indeed, as a result of losses from past disasters, these companies do not feel that they can determine actuarially fair insurance rates. In California, for example, the state itself has had to enter the insurance business to fill the gap created when private companies refused to sell earthquake insurance. The state-run pool offers less insurance coverage at higher rates than was previously offered by private insurers.
Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.

Hello my friend! I wish to say that this article is awesome, nice written and come with almost all significant infos. I?¦d like to look more posts like this .