The Net Present Value Criterion for Capital Investment Decisions

One of the most common and important decisions that firms make is to invest in new capital. Millions of dollars may be invested in a factory or machines that will last—and affect profits—for many years. The future cash flows that the investment will generate are often uncertain. And once the factory has been built, the firm usually cannot disassemble and resell it to recoup its invest- ment—it becomes a sunk cost.

How should a firm decide whether a particular capital investment is worth- while? It should calculate the present value of the future cash flows that it expects to receive from the investment and compare it with the cost of the investment. This method is known as the net present value (NPV) criterion:

Suppose a capital investment costs C and is expected to generate profits over the next 10 years of amounts p1, p2,…, p10. We then write the net present value as where R is the discount rate that we use to discount the future stream of prof- its. (R might be a market interest rate or some other rate; we will discuss how to choose it shortly.) Equation (15.3) describes the net benefit to the firm from the investment. The firm should make the investment only if that net benefit is positive—i.e., only if NPV > 0.

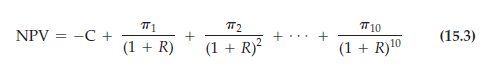
DETERMINING THE DISCOUNT RATE What discount rate should the firm use? The answer depends on the alternative ways that the firm could use its money. For example, instead of this investment, the firm might invest in another piece of capital that generates a different stream of profits. Or it might invest in a bond that yields a different return. As a result, we can think of R as the firm’s opportunity cost of capital. Had the firm not invested in this project, it could have earned a return by investing in something else. The correct value for R is therefore the return that the firm could earn on a “similar” investment.

By “similar” investment, we mean one with the same risk. As we saw in Chapter 5, the more risky an investment, the greater the return one expects to receive from it. Therefore, the opportunity cost of investing in this proj- ect is the return that one could earn from another project or asset of similar riskiness.

We’ll see how to evaluate the riskiness of an investment in the next sec- tion. For now, let’s assume that this project has no risk (i.e., the firm is sure that the future profit flows will be p1, p2, etc.). In that case, the opportunity cost of the investment is the risk-free return—e.g., the return one could earn on a government bond. If the project is expected to last for 10 years, the firm could use the annual interest rate on a 10-year government bond to com-

pute the NPV of the project, as in equation (15.3).9 If the NPV is zero, the benefit from the investment would just equal the opportunity cost, so the firm should be indifferent between investing and not investing. If the NPV is greater than zero, the benefit exceeds the opportunity cost, so the investment should be made.10

1. The Electric Motor Factory

In Section 15.1, we discussed a decision to invest $10 million in a factory to pro- duce electric motors. This factory would enable the firm to use labor and cop- per to produce 8000 motors per month for 20 years at a cost of $42.50 each. The motors could be sold for $52.50 each, for a profit of $10 per unit, or $80,000 per month. We will assume that after 20 years, the factory will be obsolete but can be sold for scrap for $1 million. Is this a good investment? To find out, we must calculate its net present value.

We will assume for now that the $42.50 production cost and the $52.50 price at which the motors can be sold are certain, so that the firm is sure that it will receive $80,000 per month, or $960,000 per year, in profit. We also assume that the $1 million scrap value of the factory is certain. The firm should therefore use a risk-free interest rate to discount future profits. Writing the cash flows in mil- lions of dollars, the NPV is

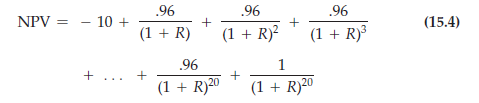
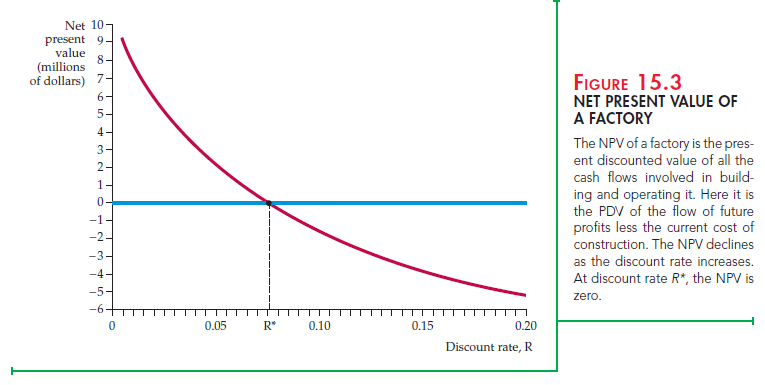
Figure 15.3 shows the NPV as a function of the discount rate R. Note that at the rate R*, which is about 7.5 percent, the NPV is equal to zero. (The rate R* is sometimes referred to as the internal rate of return on the investment.) For discount rates below 7.5 percent, the NPV is positive, so the firm should invest in the factory. For discount rates above 7.5 percent, the NPV is negative, and the firm should not invest.

2. Real versus Nominal Discount Rates

In the example above, we assumed that future cash flows are certain, so that the discount rate R should be a risk-free interest rate, such as the rate on U.S. gov- ernment bonds. Suppose that rate happened to be 9 percent. Does that mean the NPV is negative and the firm should not invest?

To answer this question, we must distinguish between real and nominal dis- count rates, and between real and nominal cash flows. Let’s begin with the cash flows. In Chapter 1, we discussed real versus nominal prices. We explained that whereas the real price is net of inflation, the nominal price includes infla- tion. In our example, we assumed that the electric motors coming out of our factory could be sold for $52.50 each over the next 20 years. We said nothing, however, about the effect of inflation. Is the $52.50 a real price, i.e., net of infla- tion, or does it include inflation? As we will see, the answer to this question can be critical.

Let’s assume that the $52.50 price—and the $42.50 production cost—are in real terms. This means that if we expect a 5-percent annual rate of infla- tion, the nominal price of the motors will increase from $52.50 in the first year to (1.05)(52.50) = $55.13 in the second year, to (1.05)(55.13) = $57.88 in the third year, and so on. Therefore, our profit of $960,000 per year is also in real terms.

Now let’s turn to the discount rate. If the cash flows are in real terms, the discount rate must also be in real terms. Why? Because the discount rate is the opportunity cost of the investment. If inflation is not included in the cash flows, it should not be included in the opportunity cost either.

In our example, the discount rate should therefore be the real interest rate on government bonds. The nominal interest rate (9 percent) is the rate that we see in the newspapers; it includes inflation. The real interest rate is the nominal rate minus the expected rate of inflation.11  If we expect inflation to be 5 percent per year on average, the real interest rate would be 9 – 5 = 4 percent. This is the discount rate that should be used to calculate the NPV of the investment in the electric motor factory. Note from Figure 15.3 that at this rate the NPV is clearly positive, so the investment should be undertaken.

When the NPV rule is used to evaluate investments, the numbers in the cal- culations may be in real or in nominal terms, as long as they are consistent. If cash flows are in real terms, the discount rate should also be in real terms. If a nominal discount rate is used, the effect of future inflation must also be included in the cash flows.

3. Negative Future Cash Flows

Factories and other production facilities can take several years to build and equip. The cost of the investment will also be spread out over several years, instead of occurring only at the outset. In addition, some investments are expected to result in losses, rather than profits, for the first few years. (For exam- ple, demand may be low until consumers learn about the product, or costs may start high and fall only when managers and workers have moved down the learning curve.) Negative future cash flows create no problem for the NPV rule; they are simply discounted, just like positive cash flows.

For example, suppose that our electric motor factory will take a year to build: $5 million is spent right away, and another $5 million is spent next year. Also, suppose the factory is expected to lose $1 million in its first year of operation and $0.5 million in its second year. Afterward, it will earn $0.96 million a year until year 20, when it will be scrapped for $1 million, as before. (All these cash flows are in real terms.) Now the net present value is

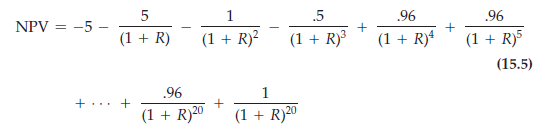
Suppose the real interest rate is 4 percent. Should the firm build this fac- tory? You can confirm that the NPV is negative, so this project is not a good investment.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.