Adjustments for Risk

We have seen that a risk-free interest rate is an appropriate discount rate for future cash flows that are certain. For most projects, however, future cash flows are far from certain. At our electric motor factory, for example, we would expect uncertainty over future copper prices, over the future demand and the price of motors, and even over future wage rates. Thus the firm cannot know what its profits from the factory will be over the next 20 years. Its best estimate of profits might be $960,000 per year, but actual profits may turn out to be higher or lower. How should the firm take this uncertainty into account when calculating the net present value of the project?

A common practice is to increase the discount rate by adding a risk premium to the risk-free rate. The idea is that the owners of the firm are risk averse, which makes future cash flows that are risky worth less than those that are certain. Increasing the discount rate takes this into account by reducing the present value of those future cash flows. But how large should the risk premium be? As we will see, the answer depends on the nature of the risk.

1. Diversifiable versus Nondiversifiable Risk

Adding a risk premium to the discount rate must be done with care. If the firm’s managers are operating in the stockholders’ interests, they must distinguish between two kinds of risk—diversifiable and nondiversifiable.12  Diversifiable risk can be eliminated by investing in many projects or by holding the stocks of many companies. Nondiversifiable risk cannot be eliminated in this way. Only nondiver- sifiable risk affects the opportunity cost of capital and should enter into the risk premium.

DIVERSIFIABLE RISK To understand this, recall from Chapter 5 that diversify- ing can eliminate many risks. For example, I cannot know whether the result of a coin flip will be heads or tails. But I can be reasonably sure that out of a thousand coin flips, roughly half will be heads. Similarly, an insurance company that sells me life insurance cannot know how long I will live. But by selling life insurance to thousands of people, it can be reasonably sure about the percentage of those who will die each year.

Much the same is true about capital investment decisions. Although the profit flow from a single investment may be very risky, overall risk will be much less if the firm invests in dozens of projects (as most large firms do). Furthermore, even if the company invests in only one project, stockholders can easily diver- sify by holding the stocks of a dozen or more different companies, or by holding a mutual fund that invests in many stocks. Thus, stockholders—the owners of the firm—can eliminate diversifiable risk.

Because investors can eliminate diversifiable risk, they cannot expect to earn a return higher than the risk-free rate by bearing it: No one will pay you for bearing a risk that there is no need to bear. And indeed, assets that have only diversifiable risk tend on average to earn a return close to the risk-free rate. Now, remember that the discount rate for a project is the opportunity cost of investing in that project rather than in some other project or asset with similar risk char- acteristics. Therefore, if the project’s only risk is diversifiable, the opportunity cost is the risk-free rate. No risk premium should be added to the discount rate.

NONDIVERSIFIABLE RISK What about nondiversifiable risk? First, let’s be clear about how such risk can arise. For a life insurance company, the possibility of a major war poses nondiversifiable risk. Because a war may increase mortal- ity rates sharply, the company cannot expect that an “average” number of its customers will die each year, no matter how many customers it has. As a result, most insurance policies, whether for life, health, or property, do not cover losses resulting from acts of war.

For capital investments, nondiversifiable risk arises because a firm’s profits tend to depend on the overall economy. When economic growth is strong, cor- porate profits tend to be higher. (For our electric motor factory, the demand for motors is likely to be strong, so profits increase.) On the other hand, profits tend to fall in a recession. Because future economic growth is uncertain, diversifica- tion cannot eliminate all risk. Investors should (and indeed can) earn higher returns by bearing this risk.

To the extent that a project has nondiversifiable risk, the opportunity cost of investing in that project is higher than the risk-free rate. Thus a risk premium must be included in the discount rate. Let’s see how the size of that risk pre- mium can be determined.

2. The Capital Asset Pricing Model

The Capital Asset Pricing Model (CAPM) measures the risk premium for a cap- ital investment by comparing the expected return on that investment with the expected return on the entire stock market. To understand the model, suppose, first, that you invest in the entire stock market (say, through a mutual fund). In that case, your investment would be completely diversified and you would bear no diversifiable risk. You would, however, bear nondiversifiable risk because the stock market tends to move with the overall economy. (The stock market reflects expected future profits, which depend in part on the economy.) As a result, the expected return on the stock market is higher than the risk-free rate. Denoting the expected return on the stock market by rm and the risk-free rate by rf, the risk

premium on the market is rm   – rf. This is the additional expected return you get for bearing the nondiversifiable risk associated with the stock market. Now consider the nondiversifiable risk associated with one asset, such as a com-pany’s stock. We can measure that risk in terms of the extent to which the return on the asset tends to be correlated with (i.e., move in the same direction as) the return on the stock market as a whole. For example, one company’s stock might have almost no correlation with the market as a whole. On average, the price of that stock would move independently of changes in the market, so it would have little or no nondi-versifiable risk. The return on that stock should therefore be about the same as the risk-free rate. Another stock, however, might be highly correlated with the market.

Its price changes might even amplify changes in the market as a whole. That stock would have substantial nondiversifiable risk, perhaps more than the stock market as a whole. If so, its return on average will exceed the market return rm.

The CAPM summarizes this relationship between expected returns and the risk premium by the following equation:

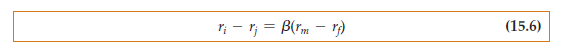
where ri  is the expected return on an asset. The equation says that the risk pre- mium on the asset (its expected return less the risk-free rate) is proportional to the risk premium on the market. The constant of proportionality, b, is called the asset beta. It measures the sensitivity of the asset’s return to market movements and, therefore, the asset’s nondiversifiable risk. If a 1-percent rise in the market tends to result in a 2-percent rise in the asset price, the beta is 2. If a 1-percent rise in the

market tends to result in a 1-percent rise in the asset price, the beta is 1. And if a 1-percent rise in the market tends to result in no change in the price of the asset, the beta is zero. As equation (15.6) shows, the larger the beta, the greater the expected return on the asset. Why? Because the asset’s nondiversifiable risk is greater.

THE RISK-ADJUSTED DISCOUNT RATE Given beta, we can determine the cor- rect discount rate to use in computing an asset’s net present value. That discount rate is the expected return on the asset or on another asset with the same risk. It is therefore the risk-free rate plus a risk premium to reflect nondiversifiable risk:

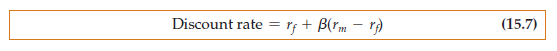
Over the past 60 years, the risk premium on the stock market, (rm   – rf), has been about 8 percent on average. If the real risk-free rate were 4 percent and beta were 0.6, the correct discount rate would be 0.04 + 0.6(0.08) = 0.09, or 9 percent.

If the asset is a stock, its beta can usually be estimated statistically.13  When the asset is a new factory, however, determining its beta is more difficult. Many firms therefore use the company cost of capital as a (nominal) discount rate. The company cost of capital is a weighted average of the expected return on the com- pany’s stock (which depends on the beta of the stock) and the interest rate that it pays for debt. This approach is correct as long as the capital investment in question is typical for the company as a whole. It can be misleading, however, if the capital investment has much more or much less nondiversifiable risk than the company as a whole. In that case, it may be better to make a reasoned guess as to how much the revenues from the investment are likely to depend on the overall economy.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.