The Value of a Bond

A bond is a contract in which a borrower agrees to pay the bondholder (the lender) a stream of money. For example, a corporate bond (a bond issued by a corporation) might make “coupon” payments of $100 per year for the next ten years, and then a principal payment of $1000 at the end of the ten-year period.4  How much would you pay for such a bond? To find out how much the bond is worth, we simply compute the present value of the payment stream:

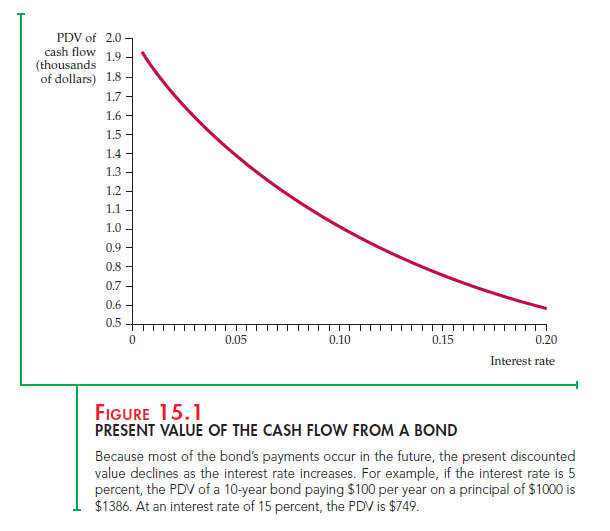
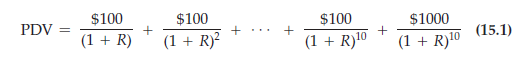
Again, the present value depends on the interest rate. Figure 15.1 shows the value of the bond—the present value of its payment stream—for interest rates up to 20 percent. Note that the higher the interest rate, the lower the value of the bond. At an interest rate of 5 percent, the bond is worth about $1386, but at an interest rate of 15 percent, its value is only $749.

1. Perpetuities

A perpetuity is a bond that pays out a fixed amount of money each year, forever. How much is a perpetuity that pays $100 per year worth? The present value of the payment stream is given by the infinite summation:

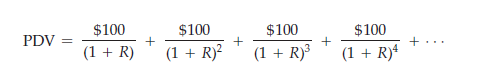
Fortunately, it isn’t necessary to calculate and add up all these terms to find the value of this perpetuity; the summation can be expressed in terms of a sim- ple formula.5

PDV =  $100/R                                                    (15.2)

So if the interest rate is 5 percent, the perpetuity is worth $100/(.05) = $2000, but if the interest rate is 20 percent, the perpetuity is worth only $500.

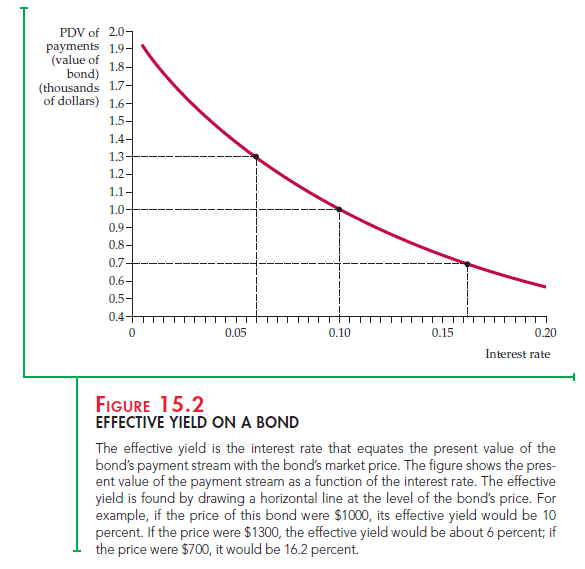
2. The Effective Yield on a Bond

Many corporate and most government bonds are traded on the bond market. The value of a traded bond can be determined directly by looking at its market price—the value placed on it by buyers and sellers.6  Thus we usually know the value of a bond, but to compare the bond with other investment opportunities, we would like to determine the interest rate consistent with that value.

EFFECTIVE YIELD Equations (15.1) and (15.2) show how the values of two different bonds depend on the interest rate used to discount future payments. These equations can be “turned around” to relate the interest rate to the bond’s value. This is particularly easy to do for the perpetuity. Suppose the market price—and thus the value—of the perpetuity is P. Then from equation (15.2), P = $100/R,  and R = $100/P.  Thus, if the price of the perpetuity is $1000, we know that the interest rate is R = $100/$1000  = 0.10, or 10 percent. This interest rate is called the effective yield, or rate of return: the percentage return that one receives by investing in a bond.

For the ten-year coupon bond in equation (15.1), calculating the effective yield is a bit more complicated. If the price of the bond is P, we write equation (15.1) as

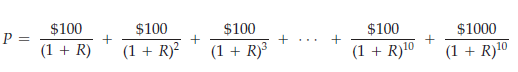
Given the price P, this equation must be solved for R. Although there is no simple formula to express R in terms of P in this case, there are methods (sometimes available on calculators and spreadsheet programs such as Excel) for calculating R numerically. Figure 15.2, which plots the same curve as that in Figure 15.1, shows how R depends on P for this ten-year coupon bond. Note that if the price of the bond is $1000, the effective yield is 10 percent. If the price rises to $1300, the effective yield drops to about 6 percent. If the price falls to $700, the effective yield rises to over 16 percent.

Yields can differ considerably among different bonds. Corporate bonds gen-erally yield more than government bonds, and as Example 15.2 shows, the bonds of some corporations yield much more than the bonds of others. One of the most important reasons for this is that different bonds carry different degrees of risk.

The U.S. government is less likely to default (fail to make interest or principal payments) on its bonds than is a private corporation. And some corporations are financially stronger and therefore less likely to default than others. As we saw in Chapter 5, the more risky an investment, the greater the return that an investor demands. As a result, riskier bonds have higher yields.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.