The rank-order tournament in the firm

1. Incentives and the Structure of a Tournament

This suggestion that a proportion of the workforce be offered a ‘prize’ (pro­motion) is an application of the incentive structure underlying the rank­order tournament. In a tournament, compensation is based not on the absolute level of individual output, but simply on the rank order of con­testants. Prizes are fixed in advance, and then allocated to contestants according to their position in the ranking. As in a sporting contest, the ‘closeness’ of the match in no way determines the rewards. Some contes­tants may be so evenly matched that separating them in the final may be a matter of the merest chance, and yet the ultimate winner may receive many times the reward of the runner-up. This type of incentive structure has been analysed by Lazear and Rosen (1981). They show that ‘under certain con­ditions, a scheme which rewards rank yields an allocation of resources iden­tical to that generated by the efficient piece rate’ (p. 863). Here, we present a very simple special case of Lazear and Rosen’s result, in order to illustrate in more detail how the tournament works.

Suppose that employees are risk neutral. Using the results of Chapter 5, it was indicated in section 2 of this chapter that if individual output is per­fectly observable, a piece-rate by which each employee receives his or her full marginal product will be efficient. The analysis up to that point had assumed only two effort levels, zero and e, but the efficiency property of the piece-rate under risk neutrality is maintained even when effort can take on a continuum of values. Since the person exerting additional effort receives the entire extra output produced under this piece-rate scheme, effort will be applied until the marginal costs incurred just equal the resulting output.

To make the example more concrete, let person fs output be directly related to his or her effort, as follows:

where nj is person j’s output, ej is person j’s level of effort, and 0j is a random element with mean zero. Further, let person j’s marginal cost of effort be represented by the expression

Clearly, the expected marginal return to an extra unit of effort is unity. The marginal cost of extra effort is simply ae_j. Thus, equating marginal cost to marginal benefit, the simple condition for maximising output net of effort costs will result in a level of effort

Now consider the case of a tournament.²² We will assume that two people are involved, persons j and k, and that their individual outputs are impos­sible to observe. Thus, although they are both risk neutral, a piece-rate scheme cannot be devised and they will be rewarded on the basis of observed effort. Even the observation of effort is subject to error, however, and we suppose for the sake of the argument that the distribution of this error is known to both people. Two prizes are set in advance (nq and n₂, with nq >n₂). The person with the highest observed effort will receive nq; the other will receive n₂. How will the behaviour of persons j and k be affected by this scheme?

As usual in neoclassical microeconomics, we expect both persons j and k to equate marginal benefits and costs of extra effort. Assume the individu­als are identical. Both will face a rising marginal cost of effort equal to ae_s or ae_k. Marginal benefits of effort are more complex to calculate, however. The gain to greater effort will derive from its effect on the probability of winning the tournament and, through this, to the expected size of the prize. Indeed, we can write the expected gain to greater effort as the product of (nq – n₂) and the change in the probability of winning the largest prize Ap. Thus

The problem for each contestant is therefore to decide how their effort affects the probability of winning the tournament. Two factors will figure most prominently in j’s decision – the accuracy of the monitor in assessing each person’s effort, and the actual level of effort chosen by person k. If person k is not working at all, the benefit to person j of exerting some pos­itive level of effort might be substantial. At a zero effort level, both k and j have a 0.5 probability of winning the tournament. Either might be per­ceived as the hardest worker and we assume that the monitor’s errors are symmetrical. Marginal benefits will exceed marginal costs of effort in this situation and person j will increase his or her work effort until they are equated. Depending on the accuracy of the monitor, person j will increase the probability of winning by working harder than k.

If k now matches the work effort of j, the probability of winning returns to 0.5 and j has to decide whether yet further effort would be worthwhile. Once more, harder work will raise the probability of winning above 0.5, but the marginal costs of effort are now higher than they were, while the mar­ginal benefits from establishing any given differential in effort levels have not changed. Person j may calculate that some attempt to distinguish him or herself from k is still worthwhile and j’s effort will rise further until mar­ginal benefits and costs are once more brought to equality. However, the differential in effort levels between j and k that maximises j’s expected payoff will be lower than it was before. Indeed, eventually, if k always responds by matching j’s effort, a point will come when both feel that there is no gain to be had from a further increase in effort. This will be the equi­librium level of effort induced by the tournament.

From Equation 6.3, it is clear that the marginal benefit of extra effort to a player in the tournament will rise with n₁ -n₂ = n* (the differential between the prizes). A larger spread can therefore be expected to increase the resulting level of effort. Similarly, a smaller value of a in Equation 6.1 will lower the marginal costs of effort and stimulate a higher equilibrium effort level.²³ Indeed, it is possible to show that with a uniform distribution of observational errors on the part of the monitor (observations of effort varying between + 2 and – 2 of their true value) the amount of effort stim­ulated by the tournament will be precisely if/a.

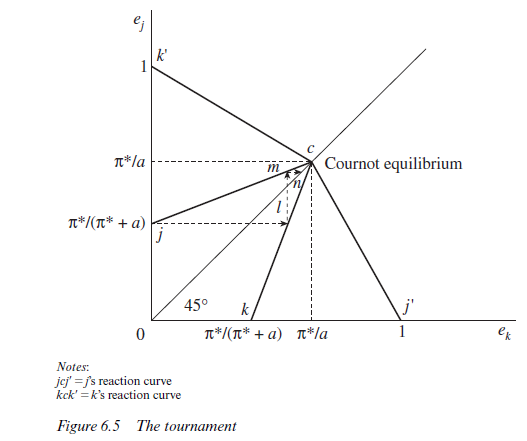
The above argument can be summarised in the form of Figure 6.5. By plotting utility maximising values of ej for different values of e_k, person j’s ‘reaction curve’ is traced out. Conversely, the optimal values of e_k corre­sponding to given levels of e_i trace out k’s ‘reaction curve’. In Figure 6.5, j’s reaction curve is labelled jcj’ while k’s reaction curve is kck’. The reaction curves of persons j and k intersect at point c. This point is called a Cournot or Nash equilibrium. Given k’s effort, person j is maximising his or her utility; and, given j’s e ffort, person k is doing the same. Neither person j nor person k will wish to move away from point c, therefore. We might envisage the approach to point c in dynamic terms, with each person responding to the moves of the other along a path such as j, l, m, n, in the diagram. Given Figure 6.5 The tournament the symmetry of the two reaction curves, it is seen that point c lies on a 45° line and hence that persons j and k end up working equally hard.

Notice that this result is a distinctive feature of the ‘rat race’. If both indi­viduals could arrange to limit their efforts, both would be better off. With e_k=ej=θ, each person will still have a 0.5 probability of winning the tour­nament and will have saved all the effort costs. The two persons could agree never to turn up to work early in the morning or to leave late at night, never to take less than an hour and a half for lunch, never to work at home, never to flatter the boss, and so forth, but if this type of agreement cannot be enforced and policed, or if we envisage each individual as competing against large numbers of other people whose behaviour is taken as largely beyond any personal influence, the efforts of each person to ‘get ahead’ will be mutually frustrating. All people finish the week tired out from their efforts to win the tournament, and none of them are any more likely to do so than they would have been had they all stayed in bed.

As seen from Equation 6.3, the amount of effort stimulated by the tour­nament depends upon π*, the difference between the two prizes. If were set equal to one, the Cournot equilibrium would involve each person exert­ing effort equal to 1/a, but this level of effort is precisely that forthcoming under the efficient piece-rate scheme outlined at the beginning of this section (Equation 6.2). Thus, the two prizes π₁ = (1/a) + 5, and     = (1/a) – 2 will

induce the same effort from the two contestants as the efficient piece-rate. Because the contestants are risk neutral, they will be equally happy under a piece-rate scheme or competing in a tournament with the prizes set so as to induce the same level of effort. Unlike the piece-rate scheme, however, the tournament does not require us to be able to measure on a cardinal scale each person’s output: it merely requires that we can rank individual perfor­mance in terms of more or less, better or worse. On the other hand, the tour­nament does require that the ‘correct’ prizes are set, and here we may once again imagine a competitive process of trial and error at work. A firm which sets > 1 will obtain greater effort from the contestants. The extra output generated by this additional effort, however, will fall short of the costs incurred by the employees, and their expected utility will fall. Thus, a firm which hits upon the ‘correct’ structure of prizes will be able to attract con­testants from firms who encourage ‘too much’ or ‘too little’ effort.

Notice the similarity between the ‘monitoring gambles’ discussed in Chapter 5, the ‘bond-posting’ incentive structure discussed in subsection 5.2 of this chapter, and the tournament. In the tournament, the employee receives (1/a) + 2 if he or she is lucky, and (1/a) – 2 if he or she is unlucky. Thus, it looks similar to any other monitoring gamble. The only difference is that receiving the bigger prize does not depend upon achieving any par­ticular satisfactory level of performance; it depends entirely on how a person performs relative to others. With the monitoring gambles of Chapter 5, all employees might have been observed working, and hence all would have their bond returned. Indeed, if a worker could never be mis­taken for an idler (q_oe = 0) all people putting in the required effort would certainly receive the larger reward. In the case of the tournament discussed above, however, one person wins and the other loses, even though they are both predicted to exert the same level of effort.

It is important to remember that our exposition of the tournament assumed that employees were risk neutral. The fact that piece-rates and tournaments can be made equivalent under these conditions does not mean that they can always be made equivalent. Risk aversion will obviously com­plicate matters considerably, and everything will depend upon the risks associated with piece-rates compared with the risks associated with the best-constructed tournament. The tournament replaces a whole distribu­tion of possible outcomes with just two prizes. In so doing, it removes many possible outcomes in the ‘middle’ of the distribution (in our example around 1/a). This will clearly not be attractive to a risk-averse person. On the other hand, the two prizes set a limit on the range of possible outcomes and may rule out extremely disastrous or very favourable occurrences, and this is obviously attractive in the context of risk aversion.²⁴ A direct com­parison between piece-rates and tournaments is not of central concern here, however. The important point is that tournaments may be a viable form of incentive structure in circumstances where piece-rates are not fea­sible because individual marginal products cannot be observed.

Lazear and Rosen’s analysis of the tournament helps to make sense of many features of hierarchical firms which would otherwise be very per­plexing. The high salaries of top corporate executives often draw adverse comment from people who correctly observe that these salaries can hardly be explained on the basis of very high productivity. ‘Productivity’, however, is not objectively measurable in many circumstances, and it seems reason­able to suppose that the observed salary structure represents a set of tour­nament prizes: ‘This interpretation suggests that presidents of large corporations do not necessarily earn high wages because they are more pro­ductive as presidents but because this particular type of payment structure makes them more productive over their entire working lives’ (p. 847). Reward at any one time will not reflect actual or even expected product. In our example, both people worked equally hard and produced the same output 1/a, yet their rewards differed, with one person getting more and the other less than his or her product. Monitoring costs will play a crucial role in determining whether or not tournaments are used. Tournaments require that each person’s performance is compared qualitatively with that of everyone else, whereas with piece-rates each person can be rewarded without reference to other people. Thus ‘salesmen, whose output level is easily observed, typically are paid by piece rates, whereas corporate execu­tives, whose output is more difficult to observe, engage in contests’ (p. 848). A similar observation was made at the end of Chapter 5, but promotion through a hierarchy was seen there as dependent upon achieving satisfac­tory effort, whereas here we are perceiving it as a prize in a tournament.

2. Further Problems with High-powered Incentives

2.1. Sabotage

One important aspect of the tournament or other ‘high-powered’ systems of incentives concerns the effect that it has on cooperative behaviour in team environments. Clearly, no participant in a tournament will have an incentive to make a colleague look good to the monitor unless such ‘selfless’ behaviour is itself fairly visible. Indeed, there is a danger that super-com­petitive ‘win at all costs’ characters might be tempted into a spot of sabo­tage. As has been noted at various points throughout the text, these ‘dysfunctional’ effects are a danger in any environment where contracts are incomplete but high-powered incentives are in place. If sabotage is costly to observe, at least part of fs effort might go into undermining the success of k rather than improving his or her own performance, and vice versa.

Sometimes, therefore, it will be necessary to weaken these temptations by adjusting downwards the spread between the prizes (‘pay compression’). Sabotage is then reduced at the price of somewhat lower effort incentives all round. If the tendency towards sabotage is partly a matter of innate ‘per­sonality’, so that very aggressive individuals (Hawks) are more prone to ‘cheat’ in this way than others (Doves), the establishment of a suitable ‘ethos’ in the firm can be a matter of great importance. A firm that screens for ‘Doves’ will be able to increase the difference between the tournament prizes at a lower cost in terms of sabotage. A firm that employs ‘Hawks’ will have to compress the differential between the prizes. Paradoxically, there­fore, Dove-employing firms can use higher-powered incentives than can Hawk-employing firms. On the other hand, ‘Hawks’ will try to infiltrate ‘Dove’ firms so that, if they cannot be successfully identified, there will be a tendency for high-incentive firms to be undermined.

This conclusion that adverse selection might work to reduce the spread of prizes in tournaments is heavily dependent on the assumption that ‘Hawks’ and ‘Doves’ are personality types and not influenced by their peers. Further, it is one thing for ‘Doves’ not to engage in sabotage but quite another for them to be fully cooperative. In a team environment, as defined by Alchian and Demsetz, encouraging active cooperation will be impor­tant. If the firm can be broken down into non-overlapping groups of people, then prizes might be awarded for relative team performance, but then sabotage between teams might still be a problem. Producing a con­tractual environment that supports cooperative effort might therefore require lower-powered incentives than would emerge from situations where individual performance is the paramount consideration. In Chapters 10 and 11, some of these issues are discussed in the context of profit-sharing and non-profit enterprise.

2.2. The crowding out of intrinsic motivation

A further possibility investigated by Frey (1994) is that a person’s ‘intrinsic motivation’ might be affected by the contractual setting of the firm. This is a subversive idea from the point of view of neoclassical economics because it calls into question the independence of a person’s ‘preferences’ from the ‘constraints’ that they face. The idea is simply that close monitoring or the payment of rewards might reduce a person’s willingness to act coopera­tively and to perform to a high standard out of a sense of professional pride, social obligation, duty or whatever words we use to describe an intrinsic desire to cooperate with others or to achieve some goal for its own sake. Extrinsic motivation concerns responses to rewards and penalties imposed from outside. It is ‘calculative’ in the conventional economic sense of comparing marginal benefits (perhaps a wage received) and marginal costs (perhaps effort expended). Intrinsic motivation concerns a desire to achieve particular ends with which the person is personally identified. Such motivation, argues Frey, ‘leads to playfulness and idiosyncrasy, convicted- ness and amateurish actions, as well as more innovativeness’ (p. 336). The problem is that extrinsic intervention in the form of incentive payments or monitoring might ‘crowd out’ intrinsically motivated behaviour. Frey (1994, p.335) gives as examples a boy who stops mowing the lawn volun­tarily after his father begins to pay him a fee, or a professor in a state uni­versity who cuts down on teaching to a minimum once the government carefully monitors her hours.

The pure psychology of this ‘crowding-out’ effect does not directly concern us here. Assuming that people do respond to intrinsic motivation and that external intervention causes this motivation to diminish, then we would expect this effect to be taken into account in any principal-agent relationship. The disciplining effect of additional monitoring or the incen­tive effect of high-powered monetary rewards would have to be traded off against the possible loss in intrinsic motivation. Frey argues, for example, that a number of propositions associated with the hypothesis of the crowd­ing out of intrinsic motivation are testable. Personal relationships between principal and agent, for example, are expected to increase the importance of intrinsic motivation as also are interesting and complex tasks. The more uniformly and highly regulated the agent, the less will be the agent’s intrin­sic motivation. Incentives via money payments will be less destructive of intrinsic motivation than close monitoring and regulation because ‘rewards shift the locus of control less than commands do’ (p.345). In other words, monetary rewards (like economic instruments of control generally) leave the agent to adjust in ways that they think are best.²⁵

Observations compatible with the crowding out of intrinsic motivation include the fact that incentive schemes are used more commonly for man­agers than for lower-level employees. The latter look at incentive schemes as a sign of lack of trust and therefore as a means of control. Morale and intrinsic motivation decline as a result. Managers are prepared to view incentive schemes more positively as a means of measuring performance. On the other hand, workers doing repetitive tasks are often rewarded by high-powered piece-rates because ‘they typically have little if any work morale which would be crowded out’ (Frey, 1995, p. 17). Similarly, payment schedules appropriate for private profit-oriented firms might be inappro­priate for a non-profit enterprise. If workers in the latter already accept lower payments in exchange for non-pecuniary intrinsic benefits, attempts to regulate and monitor too closely might be expected to be destructive of morale and of intrinsic motivation.

Source: Ricketts Martin (2002), The Economics of Business Enterprise: An Introduction to Economic Organisation and the Theory of the Firm, Edward Elgar Pub; 3rd edition.