It is 1982 and the first personal computer has recently been launched. You are assistant to the chief financial officer (CFO) of Blitzen Computers, an established computer manufacturer casting a profit-hungry eye on the PC market. You are helping the CFO evaluate the proposed introduction of the Blitzen Mark I Micro.

The Mark I’s forecasted cash flows and NPV are shown in Table 22.1. Unfortunately, the Mark I can’t meet Blitzen’s customary 20% hurdle rate and has a $46 million negative NPV, contrary to top management’s strong gut feeling that Blitzen ought to be in the personal computer market.
The CFO has called you in to discuss the project:
“The Mark I just can’t make it on financial grounds,” the CFO says. “But we’ve got to do it for strategic reasons. I’m recommending we go ahead.”
“But you’re missing the all-important financial advantage, Chief,” you reply.
“Don’t call me ‘Chief.’ What financial advantage?”
“If we don’t launch the Mark I, it will probably be too expensive to enter the micro market later, when Apple, IBM, and others are firmly established. If we go ahead, we have the opportunity to make follow-on investments that could be extremely profitable. The Mark I gives not only its own cash flows, but also a call option to go on with a Mark II micro. That call option is the real source of strategic value.”
“So it’s strategic value by another name. That doesn’t tell me what the Mark II investment’s worth. The Mark II could be a great investment or a lousy one—we haven’t got a clue.”
“That’s exactly when a call option is worth the most,” you point out perceptively. “The call lets us invest in the Mark II if it’s great and walk away from it if it’s lousy.”
“So what’s it worth?”
“Hard to say precisely, but I’ve done a back-of-the-envelope calculation, which suggests that the value of the option to invest in the Mark II could more than offset the Mark I’s $46 million negative NPV. [The calculations are shown in Table 22.2.] If the option to invest is worth $55 million, the total value of the Mark I is its own NPV, -$46 million, plus the $55 million option attached to it, or +$9 million.”
“You’re just overestimating the Mark II,” the CFO says gruffly. “It’s easy to be optimistic when an investment is three years away.”
“No, no,” you reply patiently. “The Mark II is expected to be no more profitable than the Mark I—just twice as big and therefore twice as bad in terms of discounted cash flow. I’m forecasting it to have a negative NPV of about $100 million. But there’s a chance the Mark II could be extremely valuable. The call option allows Blitzen to cash in on those upside outcomes. The chance to cash in could be worth $55 million.
“Of course, the $55 million is only a trial calculation, but it illustrates how valuable follow- on investment opportunities can be, especially when uncertainty is high and the product market is growing rapidly. Moreover, the Mark II will give us a call on the Mark III, the Mark III on the Mark IV, and so on. My calculations don’t take subsequent calls into account.”
“I think I’m beginning to understand a little bit of corporate strategy,” mumbles the CFO.
1. Questions and Answers about Blitzen’s Mark II
Question: I know how to use the Black-Scholes formula to value traded call options, but this case seems harder. What number do I use for the stock price? I don’t see any traded shares.

Answer: With traded call options, you can see the value of the underlying asset that the call is written on. Here the option is to buy a nontraded real asset, the Mark II. We can’t observe the Mark Il’s value; we have to compute it.
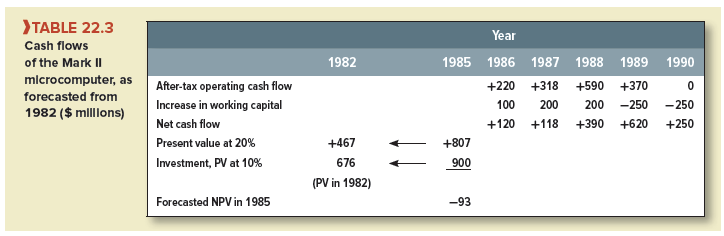
The Mark Il’s forecasted cash flows are set out in Table 22.3. The project involves an initial outlay of $900 million in 1985. The cash inflows start in the following year and have a present value of $807 million in 1985, equivalent to $467 million in 1982 as shown in Table 22.3. So the real option to invest in the Mark II amounts to a three-year call on an underlying asset worth $467 million, with a $900 million exercise price.
Notice that real options analysis does not replace DCF. You typically need DCF to value the underlying asset.
Question: Table 22.2 uses a standard deviation of 35% per year. Where does that number come from?
Answer: We recommend you look for comparables—that is, traded stocks with business risks similar to the investment opportunity.[1] For the Mark II, the ideal comparables would be growth stocks in the personal computer business or perhaps a broader sample of high-tech growth stocks. Use the average standard deviation of the comparable companies’ returns as the benchmark for judging the risk of the investment opportunity.[2]
Question: Table 22.3 discounts the Mark Il’s cash flows at 20%. I understand the high discount rate because the Mark II is risky. But why is the $900 million investment discounted at the risk-free interest rate of 10%? Table 22.3 shows the present value of the investment in 1982 of $676 million.
Answer: Black and Scholes assumed that the exercise price is a fixed, certain amount. We wanted to stick with their basic formula. If the exercise price is uncertain, you can switch to a slightly more complicated valuation formula.[3]
Question: Nevertheless, if I had to decide in 1982, once and for all, whether to invest in the Mark II, I wouldn’t do it. Right?
Answer: Right. The NPV of a commitment to invest in the Mark II is negative:
NPV(1982) = PV(cash inflows) – PV(investment) = $467 – 676 = -$209 million
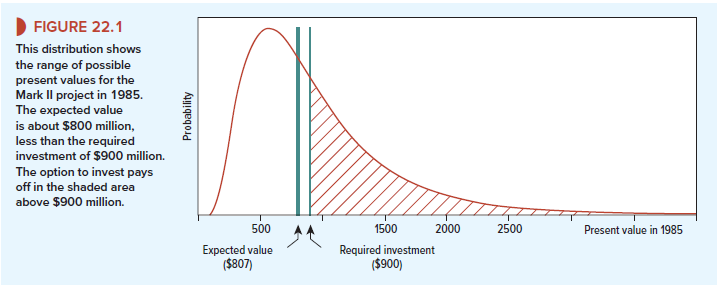
The option to invest in the Mark II is “out of the money” because the Mark II’s value is far less than the required investment. Nevertheless, the option is worth +$55 million. It is especially valuable because the Mark II is a risky project with lots of upside potential. Figure 22.1 shows the probability distribution of the possible present values of the Mark II in 1985. The expected (mean or average) outcome is our forecast of $807,[4] but the actual value could exceed $2 billion.
Question: Could it also be far below $807 million—$500 million or less?
Answer: The downside is irrelevant because Blitzen won’t invest unless the Mark II’s actual value turns out higher than $900 million. The net option payoffs for all values less than $900 million are zero.
In a DCF analysis, you discount the expected outcome ($807 million), which averages the downside against the upside, the bad outcomes against the good. The value of a call option depends only on the upside. You can see the danger of trying to value a future investment option with DCF.
Question: What’s the decision rule?
Answer: Adjusted present value. The best-case NPV of the Mark I project is -$46 million, but accepting it creates the expansion option for the Mark II. The expansion option is worth $55 million, so
APV = -46 + 55 = +$9 million
Of course, we haven’t counted other follow-on opportunities. If the Mark I and Mark II are successes, there will be an option to invest in the Mark III, possibly the Mark IV, and so on.
2. Other Expansion Options
You can probably think of many other cases where companies spend money today to create opportunities to expand in the future. A mining company may acquire rights to an ore body that is not worth developing today but could be very profitable if ore prices increase. A real estate developer may invest in worn-out farmland that could be turned into a shopping mall if a new highway is built. A pharmaceutical company may acquire a patent that gives the right but not the obligation to market a new drug. In each case, the company is acquiring a real option to expand.

24 Jun 2021
25 Jun 2021
24 Jun 2021
23 Jun 2021
25 Jun 2021
23 Jun 2021