In our examples we have assumed that cash flows occur only at the end of each year. This is sometimes the case. For example, in France and Germany, the government pays interest on its bonds annually. However, in the United States and Britain, government bonds pay interest semiannually. So if a U.S. government bond promises to pay interest of 10% a year, the investor in practice receives interest of 5% every six months.
If the first interest payment is made at the end of six months, you can earn an additional six months’ interest on this payment. For example, if you invest $100 in a bond that pays interest of 10% compounded semiannually, your wealth will grow to 1.05 X $100 = $105 by the end of six months and to 1.05 X $105 = $110.25 by the end of the year. In other words, an interest rate of 10% compounded semiannually is equivalent to 10.25% compounded annually. The effective annual interest rate on the bond is 10.25%.
Let’s take another example. Suppose a bank offers you an automobile loan at an annual percentage rate, or APR, of 12% with interest to be paid monthly. By this the bank means that each month you need to pay one-twelfth of the annual rate, that is, 12/12 = 1% a month. Thus the bank is quoting a rate of 12%, but the effective annual interest rate on your loan is 1.0112 – 1 = .1268 or 12.68%.[1]
Our examples illustrate that you need to distinguish between the quoted annual interest rate and the effective annual rate. The quoted annual rate is usually calculated as the total annual payment divided by the number of payments in the year. When interest is paid once a year, the quoted and effective rates are the same. When interest is paid more frequently, the effective interest rate is higher than the quoted rate.
In general, if you invest $1 at a rate of r per year compounded m times a year, your investment at the end of the year will be worth [1 + (r/m)]m and the effective interest rate is [1 + (r/m)]m – 1. In our automobile loan example r = .12 and m = 12. So the effective annual interest rate was [1 + .12/12]12 – 1 = .1268, or 12.68%.
1. Continuous Compounding
Instead of compounding interest monthly or semiannually, the rate could be compounded weekly (m = 52) or daily (m = 365). In fact, there is no limit to how frequently interest could be paid. One can imagine a situation where the payments are spread evenly and continuously throughout the year, so the interest rate is continuously compounded.9 In this case m is infinite.
It turns out that there are many occasions in finance when continuous compounding is useful. For example, one important application is in option pricing models, such as the Black- Scholes model that we introduce in Chapter 21. These are continuous time models. So you will find that most computer programs for calculating option values ask for the continuously compounded interest rate.
It may seem that a lot of calculations would be needed to find a continuously compounded interest rate. However, think back to your high school algebra. You may recall that as m approaches infinity [1 + (r/m)]m approaches (2.718)r . The figure 2.718—or e, as it is called—is the base for natural logarithms. Therefore, $1 invested at a continuously compounded rate of r will grow to er = (2.718)r by the end of the first year. By the end of t years it will grow to ert = (2.718)rt.
Example 1 Suppose you invest $1 at a continuously compounded rate of 11% (r = .11) for one year (t = 1). The end-year value is e11, or $1.116. In other words, investing at 11% a year continuously compounded is exactly the same as investing at 11.6% a year annually compounded.
Example 2 Suppose you invest $1 at a continuously compounded rate of 11% (r = .11) for two years (t = 2). The final value of the investment is ert = e22, or $1.246.
Sometimes it may be more reasonable to assume that the cash flows from a project are spread evenly over the year rather than occurring at the year’s end. It is easy to adapt our previous formulas to handle this. For example, suppose that we wish to compute the present value of a perpetuity of C dollars a year. We already know that if the payment is made at the end of the year, we divide the payment by the annually compounded rate of r:
![]()
If the same total payment is made in an even stream throughout the year, we use the same formula but substitute the continuously compounded rate.
Suppose the annually compounded rate is 18.5%. The present value of a $100 perpetuity, with each cash flow received at the end of the year, is 100/.185 = $540.54. If the cash flow is received continuously, we must divide $100 by 17%, because 17% continuously compounded is equivalent to 18.5% annually compounded (e17 = 1.185). The present value of the continuous cash flow stream is 100/.17 = $588.24. Investors are prepared to pay more for the continuous cash payments because the cash starts to flow in immediately.
Example 3 After you have retired, you plan to spend $200,000 a year for 20 years. The annually compounded interest rate is 10%. How much must you save by the time you retire to support this spending plan?
Let us first do the calculations assuming that you spend the cash at the end of each year. In this case we can use the simple annuity formula that we derived earlier:
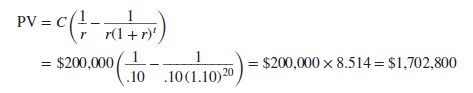
Thus, you will need to have saved $1.7 million by the time you retire.
Instead of waiting until the end of each year before you spend any cash, it is more reasonable to assume that your expenditure will be spread evenly over the year. In this case, instead of using the annually compounded rate of 10%, we must use the continuously compounded rate of r = 9.53% (e0953 = 1.10). Therefore, to cover a steady stream of expenditure, you need to set aside the following sum:[1]
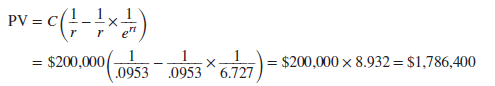
To support a steady stream of outgoings, you must save an additional $83,600.
Often in finance you need only a ballpark estimate of present value. An error of 5% in a present value calculation may be perfectly acceptable. In such cases it doesn’t usually matter whether you assume that cash flows occur at the end of the year or in a continuous stream. At other times precision matters, and you do need to worry about the exact frequency of the cash flows.
Source: Brealey Richard A., Myers Stewart C., Allen Franklin (2020), Principles of Corporate Finance, McGraw-Hill Education; 13th edition.

Some genuinely excellent information, Gladiolus I detected this.