An Overview—The Efficiency of Competitive Markets

Our analysis of general equilibrium and economic efficiency is now complete. In the process, we have obtained two remarkable results. First, we have shown that for any initial allocation of resources, a competitive process of exchange among individuals, whether through exchange, input markets, or output markets, will lead to a Pareto efficient outcome. The first theorem of welfare economics tells us that a competitive system, building on the self-interested goals of consumers and producers and on the ability of market prices to convey information to both parties, will achieve a Pareto efficient allocation of resources.

Second, we have shown that with indifference curves that are convex, any efficient allocation of resources can be achieved by a competitive process with a suitable redistribution of those resources. Of course, there may be many Pareto efficient outcomes. But the second theorem of welfare economics tells us that under certain (admittedly ideal) conditions, issues of equity and efficiency can be treated distinctly from one another. If we are willing to put equity issues aside, then we know that there is a competitive equilibrium that maximizes con­sumer and producer surplus, i.e., is economically efficient.

Both theorems of welfare economics depend crucially on the assumption that markets are competitive. Unfortunately, neither of these results necessarily holds when, for some reason, markets are no longer competitive. In the next two chapters, we will discuss ways in which markets fail and what government can do about it. Before proceeding, however, it is essential to review our understanding of the workings of the competitive process. We thus list the conditions required for economic efficiency in exchange, in input markets, and in output markets.

These conditions are important; in each of these three cases, you should review the explanation of the conditions in this chapter and the underlying building blocks in prior chapters.

1. Efficiency in exchange: All allocations must lie on the exchange contract curve so that every consumer ’s marginal rate of substitution of food for clothing is the same:

A competitive market achieves this efficient outcome because, for consum- ers, the tangency of the budget line and the highest attainable indifference curve ensure that:

2. Efficiency in the use of inputs in production: Every producer ’s marginal rate of technical substitution of labor for capital is equal in the production of both goods:

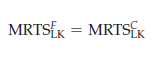
A competitive market achieves this technically efficient outcome because each producer maximizes profit by choosing labor and capital inputs so that the ratio of the input prices is equal to the marginal rate of technical substitution:

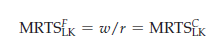
3. Efficiency in the output market: The mix of outputs must be chosen so that the marginal rate of transformation between outputs is equal to consumers’ marginal rates of substitution:

A competitive market achieves this efficient outcome because profit- maximizing producers increase their output to the point at which marginal cost equals price:

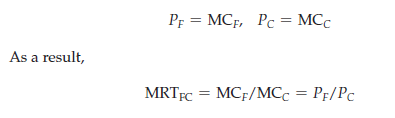
But consumers maximize their satisfaction in competitive markets only if and the output efficiency conditions are satisfied. Thus efficiency requires that goods be produced in combinations and at costs that match people’s willingness to pay for them.

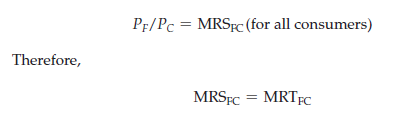
Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.