We will return to our $10 million electric motor factory in Section 15.4, but first we must address a basic problem: How much is $1 paid in the future worth today? The answer depends on the interest rate: the rate at which one can borrow or lend money.
Suppose the annual interest rate is R. (Don’t worry about which interest rate this actually is; later, we’ll discuss the various types of interest rates.) Then $1 today can be invested to yield (1 + R) dollars a year from now. Therefore, 1 + R dollars is the future value of $1 today. Now, what is the value today, i.e., the present discounted value (PDV), of $1 paid one year from now? The answer is easy: because 1 + R dollars one year from now is worth (1 + R)/(1 + R) = $1 today, $1 a year from now is worth $1/(1 + R) today. This is the amount of money that will yield $1 after one year if invested at the rate R.
What is the value today of $1 paid two years from now? If $1 were invested today at the interest rate R, it would be worth 1 + R dollars after one year, and (1 + R)(1 + R) = (1 + R)2 dollars at the end of two years. Because (1 + R)2 dollars two years from now is worth $1 today, $1 two years from now is worth $1/(1 + R)2 today. Similarly, $1 paid three years from now is worth $1/(1 + R)3 today, and $1 paid n years from now is worth $1/(1 + R)n today.
We can summarize this as follows:
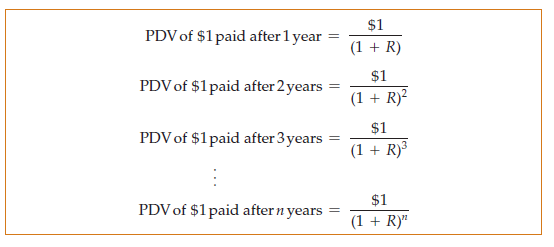
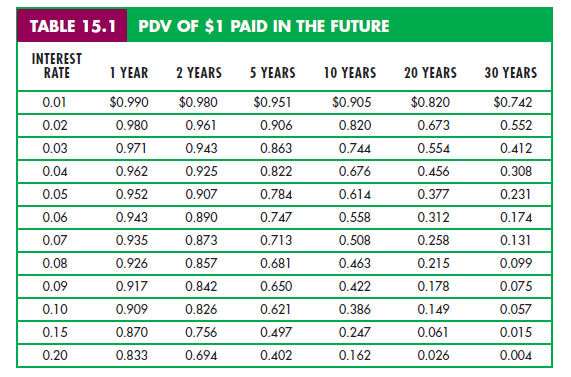
Table 15.1 shows, for different interest rates, the present value of $1 paid after 1, 2, 5, 10, 20, and 30 years. Note that for interest rates above 6 or 7 percent, $1paid 20 or 30 years fro m now is worth very little today. But this is not the case for low interest rates. For example, if R is 3 percent, the PDV of $1 paid 20 years from now is about 55 cents. In other words, if 55 cents were invested now at the rate of 3 percent, it would yield about $1 after 20 years.
1. Valuing Payment Streams
We can now determine the present value of a stream of payments over time. For example, consider the two payment streams in Table 15.2. Stream A comes to $200: $100 paid now and $100 a year from now. Stream B comes to $220: $20 paid now, $100 a year from now, and $100 two years from now. Which payment stream would you prefer to receive? The answer depends on the interest rate.
To calculate the present discounted value of these two streams, we compute and add the present values of each year’s payment:
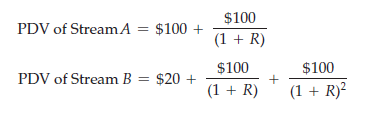
Table 15.3 shows the present values of the two streams for interest rates of 5, 10, 15, and 20 percent. As the table shows, the preferred stream depends on the interest rate. For interest rates of 10 percent or less, Stream B is worth more; for interest rates of 15 percent or more, Stream A is worth more. Why? Because even though less is paid out in Stream A, it is paid out sooner.


This simple example shown in Tables 15.2 and 15.3 illustrates an important principle. The present value of a stream of payments depends on three things: (1) the amount of each payment, (2) the timing of the payments, and (3) the interest rate used to discount payments made in the future. As we will see, this principle applies to a wide variety of problems.
Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.

Well I really liked reading it. This subject provided by you is very helpful for proper planning.
Wohh just what I was looking for, thanks for putting up.