A Nash equilibrium is a noncooperative equilibrium: Each firm makes the decisions that give it the highest possible profit, given the actions of its competitors. As we have seen, the resulting profit earned by each firm is higher than it would be under perfect competition but lower than if the firms colluded.
Collusion, however, is illegal, and most managers prefer to stay out of jail. But if cooperation can lead to higher profits, why don’t firms cooperate without explicitly colluding? In particular, if you and your competitor can both figure out the profit-maximizing price you would agree to charge if you were to collude, why not just set that price and hope your competitor will do the same? If your competitor does do the same, you will both make more money.
The problem is that your competitor probably won’t choose to set price at the collusive level. Why not? Because your competitor would do better by choosing a lower price, even if it knew that you were going to set price at the collusive level.
To understand this, let’s go back to our example of price competition from the last section. The firms in that example each have a fixed cost of $20, have zero variable cost, and face the following demand curves:
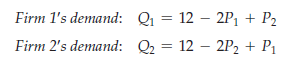
We found that in the Nash equilibrium each firm will charge a price of $4 and earn a profit of $12, whereas if the firms collude, they will charge a price of $6 and earn a profit of $16. Now suppose that the firms do not collude, but that Firm 1 charges the $6 collusive price, hoping that Firm 2 will do the same. If Firm 2 does do the same, it will earn a profit of $16. But what if it charges the $4 price instead? In that case, Firm 2 would earn a profit of
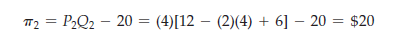
Firm 1, on the other hand, will earn a profit of only
![]()
So if Firm 1 charges $6 but Firm 2 charges only $4, Firm 2’s profit will increase to $20. And it will do so at the expense of Firm 1’s profit, which will fall to $4. Clearly, Firm 2 does best by charging only $4. Similarly, Firm 1 does best by charging only $4. If Firm 2 charges $6 and Firm 1 charges $4, Firm 1 will earn a $20 profit and Firm 2 only $4.
PAYOFF MATRIX Table 12.3 summarizes the results of these different possibili- ties. In deciding what price to set, the two firms are playing a noncooperative game: Each firm independently does the best it can, taking its competitor into account. Table 12.3 is called the payoff matrix for this game because it shows the profit (or payoff) to each firm given its decision and the decision of its competitor. For example, the upper left-hand corner of the payoff matrix tells us that if both firms charge $4, each will make a $12 profit. The upper right-hand corner tells us that if Firm 1 charges $4 and Firm 2 charges $6, Firm 1 will make $20 and Firm 2 $4.
This payoff matrix can clarify the answer to our original question: Why don’t firms behave cooperatively, and thereby earn higher profits, even if they can’t collude? In this case, cooperating means both firms charging $6 instead of $4 and thereby earning $16 instead of $12. The problem is that each firm always makes more money by charging $4, no matter what its competitor does. As the pay- off matrix shows, if Firm 2 charges $4, Firm 1 does best by charging $4. And if Firm 2 charges $6, Firm 1 still does best by charging $4. Similarly, Firm 2 always does best by charging $4, no matter what Firm 1 does. As a result, unless the two firms can sign an enforceable agreement to charge $6, neither firm can expect its competitor to charge $6, and both will charge $4.
THE PRISONERS’ DILEMMA A classic example in game theory, called the pris- oners’ dilemma, illustrates the problem faced by oligopolistic firms. It goes as follows: Two prisoners have been accused of collaborating in a crime. They are in separate jail cells and cannot communicate with each other. Each has been asked to confess. If both prisoners confess, each will receive a prison term of five years. If neither confesses, the prosecution’s case will be difficult to make, so the prisoners can expect to plea bargain and receive terms of two years. On the other hand, if one prisoner confesses and the other does not, the one who confesses will receive a term of only one year, while the other will go to prison for 10 years. If you were one of these prisoners, what would you do—confess or not confess?
The payoff matrix in Table 12.4 summarizes the possible outcomes. (Note that the “payoffs” are negative; the entry in the lower right-hand corner means a two-year sentence for each prisoner.) As the table shows, our prisoners face a dilemma. If they could both agree not to confess (in a way that would be bind- ing), then each would go to jail for only two years. But they can’t talk to each other, and even if they could, can they trust each other? If Prisoner A does not confess, he risks being taken advantage of by his former accomplice. After all, no matter what Prisoner A does, Prisoner B comes out ahead by confessing. Likewise, Prisoner A always comes out ahead by confessing, so Prisoner B must worry that by not confessing, she will be taken advantage of. Therefore, both prisoners will probably confess and go to jail for five years.


Oligopolistic firms often find themselves in a prisoners’ dilemma. They must decide whether to compete aggressively, attempting to capture a larger share of the market at their competitor ’s expense, or to “cooperate” and compete more passively, coexisting with their competitors and settling for their current market share, and perhaps even implicitly colluding. If the firms compete passively, set- ting high prices and limiting output, they will make higher profits than if they compete aggressively.
Like our prisoners, however, each firm has an incentive to “fink” and undercut its competitors, and each knows that its competitors have the same incentive. As desirable as cooperation is, each firm worries—with good reason—that if it com- petes passively, its competitor might decide to compete aggressively and seize the lion’s share of the market. In the pricing problem illustrated in Table 12.3, both firms do better by “cooperating” and charging a high price. But the firms are in a prisoners’ dilemma, where neither can trust its competitor to set a high price.
Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.

Wow, amazing blog layout! How long have you been blogging for? you made blogging look easy. The overall look of your web site is excellent, let alone the content!