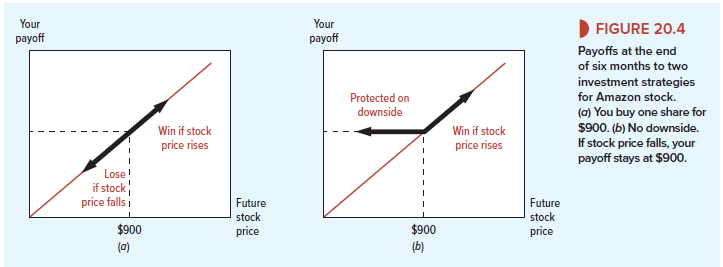
Look now at Figure 20.4a, which shows the payoff if you buy Amazon stock at $900. You gain dollar-for-dollar if the stock price goes up and you lose dollar-for-dollar if it falls. That’s trite; it doesn’t take a genius to draw a 45-degree line.
Look now at panel (b), which shows the payoffs from an investment strategy that retains the upside potential of Amazon stock but gives complete downside protection. In this case, your payoff stays at $900 even if the Amazon stock price falls to $800, $500, or zero. Panel (b)’s payoffs are clearly better than panel (a)’s. If a financial alchemist could turn panel (a) into panel (b), you’d be willing to pay for the service.
Now, as you have probably suspected, this financial alchemy is for real. You can do the transmutation shown in Figure 20.4. You do it with options, and we will show you how. Look at row 1 of Figure 20.5. The first diagram again shows the payoff from buying a share of Amazon stock, while the next diagram in row 1 shows the payoffs from buying an Amazon put option with an exercise price of $900. The third diagram shows the effect of combining these two positions. You can see that if Amazon’s stock price rises above $900, your put option is valueless, so you simply receive the gains from your investment in the share. However, if the stock price falls below $900, you can exercise your put option and sell your stock for $900. Thus, by adding a put option to your investment in the stock, you have protected yourself against loss.[1] This is the strategy that we depicted in Figure 20.4. Of course, there is no gain without pain. The cost of insuring yourself against loss is the amount that you pay for a put option on Amazon stock with an exercise price of $900. In April 2017, the price of this put was $59.55. This was the going rate for financial alchemists.
We have just seen how put options can be used to provide downside protection. We now show you how call options can be used to get the same result. This is illustrated in row 2 of Figure 20.5. The first diagram shows the payoff from placing the present value of $900 in a bank deposit. Regardless of what happens to the price of Amazon stock, your bank deposit will pay off $900. The second diagram in row 2 shows the payoff from a call option on Amazon stock with an exercise price of $900, and the third diagram shows the effect of combining these two positions. Notice that if the price of Amazon stock falls, your call is worthless, but you still have your $900 in the bank. For every dollar that Amazon stock price rises above $900, your investment in the call option pays off an extra dollar. For example, if the stock price rises to $980, you will have $900 in the bank and a call worth $80. Thus you participate fully in any rise in the price of the stock, while being fully protected against any fall. So we have just found another way to provide the downside protection depicted in panel (b) of Figure 20.4.
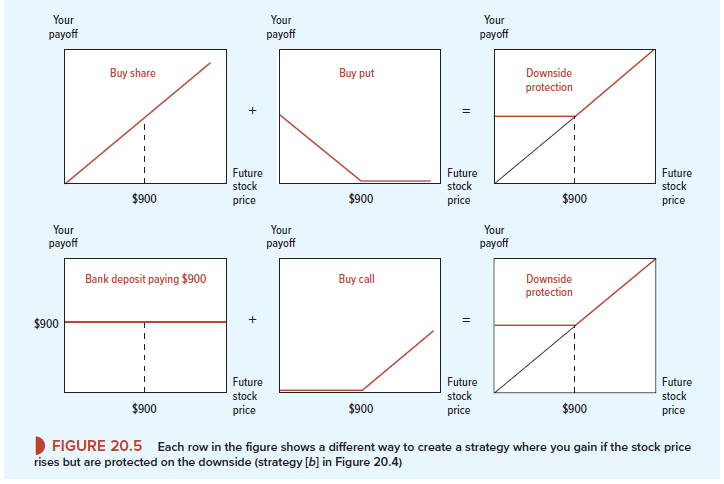
These two rows of Figure 20.5 tell us something about the relationship between a call option and a put option. Regardless of the future stock price, both investment strategies provide identical payoffs. In other words, if you buy the share and a put option to sell it for $900, you receive the same payoff as from buying a call option and setting enough money aside to pay the $900 exercise price. Therefore, if you are committed to holding the two packages until the options expire, the two packages should sell for the same price today. This gives us a fundamental relationship for European options:
Value of call + present value of exercise price = value of put + share price
To repeat, this relationship holds because the payoff of
buy call, invest present value of exercise price in safe asset8
is identical to the payoff from
buy put, buy share.
This basic relationship among share price, call and put values, and the present value of the exercise price is called put-call parity.
Put-call parity can be expressed in several ways. Each expression implies two investment strategies that give identical results. For example, suppose that you want to solve for the value of a put. You simply need to twist the put-call parity formula around to give
Value of put = value of call + present value of exercise price – share price
From this expression you can deduce that
buy put
is identical to
buy call, invest present value of exercise price in safe asset, sell share.
In other words, if puts are not available, you can get exactly the same payoff by buying calls, putting cash in the bank, and selling shares.
If you find this difficult to believe, look at Figure 20.6, which shows the possible payoffs from each position. The diagram on the left shows the payoffs from a call option on Amazon stock with an exercise price of $900. The second diagram shows the payoffs from placing the present value of $900 in the bank. Regardless of what happens to the share price, this investment will pay off $900. The third diagram shows the payoffs from selling Amazon stock. When you sell a share that you don’t own, you have a liability—you must sometime buy it back. As they say on Wall Street:
He who sells what isn’t his’n
Buys it back or goes to pris’n
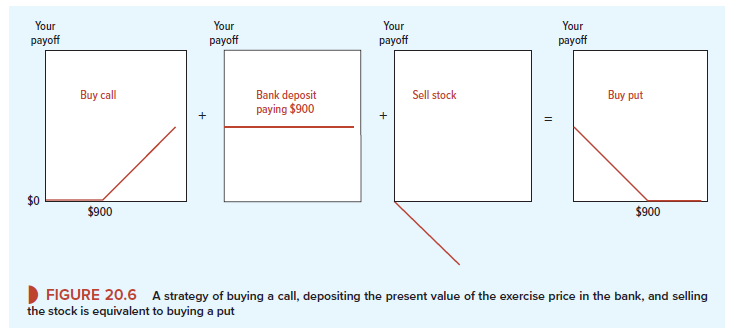
Therefore, the best that can happen to you is that the share price falls to zero. In that case, it costs you nothing to buy the share back. But for every extra dollar on the future share price, you will need to spend an extra dollar to buy the share. The final diagram in Figure 20.6 shows that the total payoff from these three positions is the same as if you had bought a put option. For example, suppose that when the option matures, the stock price is $800. Your call will be worthless, your bank deposit will be worth $900, and it will cost you $800 to repurchase the share. Your total payoff is 0 + 900 – 800 = $100, exactly the same as the payoff from the put.
If two investments offer identical payoffs, then they should sell for the same price today. If the law of one price is violated, you have a potential arbitrage opportunity. So let’s check whether there are any arbitrage profits to be made from our Amazon calls and puts. In April 2017, the price of a six-month call with a $900 exercise price was $64.30, the interest rate was about .5% for 6 months, and the price of Amazon stock was $900. Therefore the cost of a homemade put was
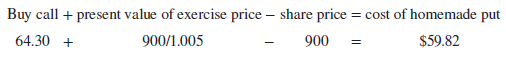
This is almost exactly the same as it would have cost you to buy a put directly.
1. Spotting the Option
Options rarely come with a large label attached. Often, the trickiest part of the problem is to identify the option. When you are not sure whether you are dealing with a put or a call or a complicated blend of the two, it is a good precaution to draw a position diagram. Here is an example.
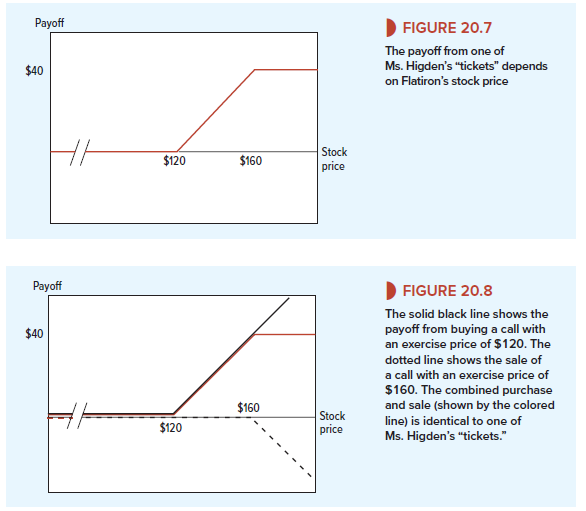
The Flatiron and Mangle Corporation has offered its president, Ms. Higden, the following incentive scheme: At the end of the year Ms. Higden will be paid a bonus of $50,000 for every dollar that the price of Flatiron stock exceeds its current figure of $120. However, the maximum bonus that she can receive is set at $2 million.[3]
You can think of Ms. Higden as owning 50,000 tickets, each of which pays nothing if the stock price fails to beat $120. The value of each ticket then rises by $1 for each dollar rise in the stock price up to the maximum of $2,000,000/50,000 = $40. Figure 20.7 shows the payoffs from just one of these tickets. The payoffs are not the same as those of the simple put and call options that we drew in Figure 20.1, but it is possible to find a combination of options that exactly replicates Figure 20.7. Before going on to read the answer, see if you can spot it yourself. (If you are someone who enjoys puzzles of the make-a-triangle-from-just-two- matchsticks type, this one should be a walkover.)
The answer is in Figure 20.8. The solid black line represents the purchase of a call option with an exercise price of $120, and the dotted line shows the sale of another call option with an exercise price of $160. The colored line shows the payoffs from a combination of the purchase and the sale—exactly the same as the payoffs from one of Ms. Higden’s tickets.
Thus, if we wish to know how much the incentive scheme is costing the company, we need to calculate the difference between the value of 50,000 call options with an exercise price of $120 and the value of 50,000 calls with an exercise price of $160.
We could have made the incentive scheme depend in a much more complicated way on the stock price. For example, the bonus could peak at $2 million and then fall steadily back to zero as the stock price climbs above $160.n You could still have represented this scheme as a combination of options. In fact, we can state a general theorem:
Any set of contingent payoffs—that is, payoffs that depend on the value of some other asset—can be constructed with a mixture of simple options on that asset.
In other words, you can create any position diagram—with as many ups and downs or peaks and valleys as your imagination allows—by buying or selling the right combinations of puts and calls with different exercise prices.[4] [5]
Finance pros often talk about financial engineering, which is the practice of packaging different investments to create new tailor-made instruments. Perhaps a German company would like to set a minimum and maximum cost at which it can buy dollars in six-months’ time. Or perhaps an oil company would like to pay a lower rate of interest on its debt if the price of oil falls. Options provide the building blocks that financial engineers use to create these interesting payoff structures.

I consider something really interesting about your web site so I saved to fav.
Hi my loved one! I want to say that this post is amazing, nice written and include almost all significant infos. I¦d like to see more posts like this .