More Shortcuts – Growing Perpetuities and Annuities

1. Growing Perpetuities

You now know how to value level streams of cash flows, but you often need to value a stream of cash flows that grows at a constant rate. For example, think back to your plans to donate $10 billion to fight malaria and other infectious diseases. Unfortunately, you made no allowance for the growth in salaries and other costs, which will probably average about 4% a year starting in year 1. Therefore, instead of providing $1 billion a year in perpetuity, you must provide $1 billion in year 1, 1.04 x $1 billion in year 2, and so on. If we call the growth rate in costs g, we can write down the present value of this stream of cash flows as follows:

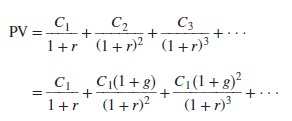
Fortunately, there is a simple formula for the sum of this geometric series.⁶ If we assume that r is greater than g, our clumsy-looking calculation simplifies to

Therefore, if you want to provide a perpetual stream of income that keeps pace with the growth rate in costs, the amount that you must set aside today is

You will meet this perpetual-growth formula again in Chapter 4, where we use it to value the stocks of mature, slowly growing companies.

2. Growing Annuities

Example 2.6 • Winning Big at the Lottery

In August 2017, a Massachusetts woman invested in a Powerball lottery ticket and won a record $758.7 million. We suspect that she received unsolicited congratulations, good wishes, and requests for money from dozens of more or less worthy charities, relations, and newly devoted friends. In response, she could fairly point out that the prize wasn’t really worth $758.7 million. That sum was to be paid in 30 annual installments. The payment in the first year was only $11.42 million, but it then increased each year by 5% so that the final payment was $47.00 mil­lion. The total amount paid out was $758.7 million, but the winner had to wait to get it.

If the interest rate was 2.7%, what was that $758.7 prize really worth? Suppose that the first payment occurs at the end of year 1, so that C₁ = $11.42 million. If the payments then grow at the rate of g = .05 each year, the payment in year 2 is 11.42 x 1.05, and in year 3 it is 11.42 x 1.05². Of course, you could calculate each of the 30 cash flows and discount them at 2.7%. The alternative is to use the following formula for the present value of a growing annuity:

In the case of our lottery, the present value of the growing stream of payments is

Thus, the present value of a growing stream of payments starting at the end of the first year is $468 million. In practice, the news is not quite that bad because the lottery winner receives the first payment immediately (in year 0) and the last one is received in year 29 rather than in year 30. Therefore, we need to increase our estimate of present value by 1 + r. So the present value of the prize is 468 × 1.027 = $481 million.

If the total Powerball prize money was paid out immediately, it would be worth $757.8 million. Paying out this money over the next 29 years reduces the value of the prize to $481 million, much below the well-trumpeted prize but still not a bad day’s haul.

For winners with big spending plans, lottery operators generally make arrangements so that they may take an equivalent lump sum. In our example, the winner could either take the $758.7 million spread over 30 years or receive $481 million up front. Both arrangements had the same present value.

Too many formulas are bad for the digestions. So we will stop at this point and spare you any more of them. The formulas discussed so far appear in Table 2.2.

Source:  Brealey Richard A., Myers Stewart C., Allen Franklin (2020), Principles of Corporate Finance, McGraw-Hill Education; 13th edition.