1. How to Value Perpetuities
Sometimes there are shortcuts that make it easy to calculate present values. Let us look at some examples.
On occasion, the British and the French have been known to disagree and sometimes even to fight wars. At the end of some of these wars the British consolidated the debt they had issued during the war. The securities issued in such cases were called consols. Consols are perpetuities. They are bonds that the government is under no obligation to repay but that offer a fixed income for each year to perpetuity. The British government is still paying interest on consols issued all those years ago. The annual rate of return on a perpetuity is equal to the promised annual payment divided by the present value:

We can obviously twist this around and find the present value of a perpetuity given the discount rate r and the cash payment C:4
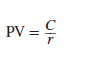
The year is 2030. You have been fabulously successful and are now a billionaire many times over. It was fortunate indeed that you took that finance course all those years ago. You have decided to follow in the footsteps of two of your philanthropic heroes, Bill Gates and Warren Buffett. Malaria is still a scourge and you want to help eradicate it and other infectious diseases by endowing a foundation to combat these diseases. You aim to provide $1 billion a year in perpetuity, starting next year. So, if the interest rate is 10%, you need to write a check today for
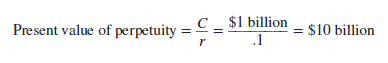
Two warnings about the perpetuity formula. First, at a quick glance, you can easily confuse the formula with the present value of a single payment. A payment of $1 at the end of one year has a present value of 1/(1 + r). The perpetuity has a value of 1/r. These are quite different.
Second, the perpetuity formula tells us the value of a regular stream of payments starting one period from now. Thus your $10 billion endowment would provide the foundation with its first payment in one year’s time. If you also want to provide an up-front sum, you will need to lay out an extra $1 billion.

Sometimes you may need to calculate the value of a perpetuity that does not start to make payments for several years. For example, suppose that you decide to provide $1 billion a year with the first payment four years from now. Figure 2.6 provides a timeline of these payments. Think first about how much they will be worth in year 3. At that point the endowment will be an ordinary perpetuity with the first payment due at the end of the year. So our perpetuity formula tells us that in year 3 the endowment will be worth $1/r = $1/.1 = $10 billion. But it is not worth that much now. To find today’s value we need to multiply by the three-year discount factor 1/(1 + r)3 = 1/(1.1)3 = .751. Thus, the “delayed” perpetuity is worth $10 billion x .751 = $7.51 billion. The full calculation is:
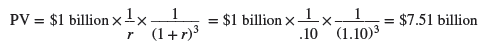
2. How to Value Annuities
An annuity is an asset that pays a fixed sum each year for a specified number of years. The equal-payment house mortgage or installment credit agreement are common examples of annuities. So are interest payments on most bonds, as we shall see in the next chapter.
You can always value an annuity by calculating the value of each cash flow and finding the total. However, it is often quicker to use a simple formula that states that if the interest rate is r, then the present value of an annuity that pays $C a period for each of t periods is:
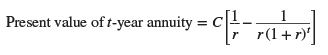
The expression in brackets shows the present value of $1 a year for each of t years. It is generally known as the t-year annuity factor.
If you are wondering where this formula comes from, look at Figure 2.7. It shows the payments and values of three investments.
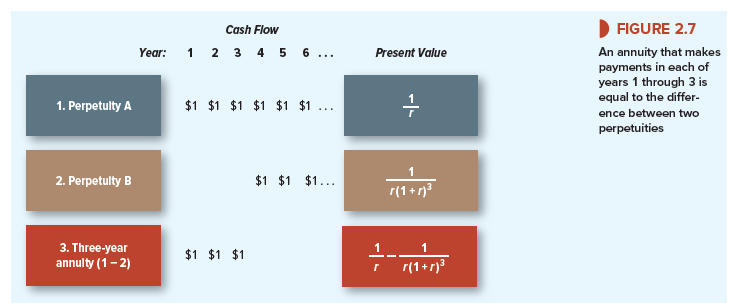
Row 1 The investment in the first row provides a perpetual stream of $1 starting at the end of the first year. We have already seen that this perpetuity has a present value of 1/r.
Row 2 Now look at the investment shown in the second row of Figure 2.7. It also provides a perpetual stream of $1 payments, but these payments don’t start until year 4. This stream of payments is identical to the payments in row 1, except that they are delayed for an additional three years. In year 3, the investment will be an ordinary perpetuity with payments starting in one year and will therefore be worth 1/r in year 3. To find the value today, we simply multiply this figure by the three-year discount factor. Thus, as we saw earlier
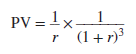
Row 3 Finally, look at the investment shown in the third row of Figure 2.7. This provides a level payment of $1 a year for each of three years. In other words, it is a three-year annuity. You can also see that, taken together, the investments in rows 2 and 3 provide exactly the same cash payments as the investment in row 1. Thus the value of our annuity (row 3) must be equal to the value of the row 1 perpetuity less the value of the delayed row 2 perpetuity:
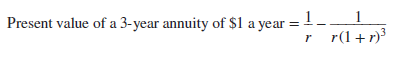
Remembering formulas is about as difficult as remembering other people’s birthdays. But as long as you bear in mind that an annuity is equivalent to the difference between an immediate and a delayed perpetuity, you shouldn’t have any difficulty.5
Example 2.2 • Costing an Installment Plan
Most installment plans call for level streams of payments. Suppose that Tiburon Autos offers an “easy payment” scheme on a new Toyota of $5,000 a year, paid at the end of each of the next five years, with no cash down. What is the car really costing you?
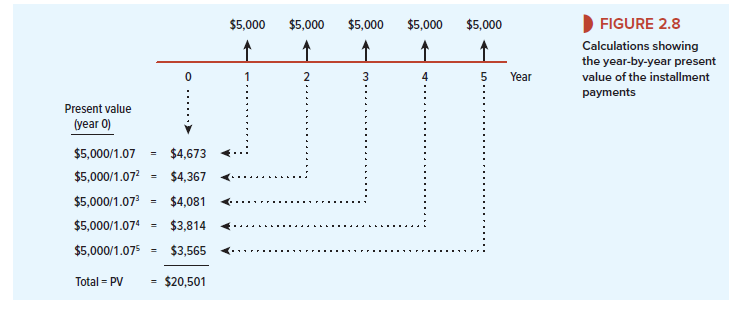
First let us do the calculations the slow way, to show that if the interest rate is 7%, the present value of these payments is $20,501. The timeline in Figure 2.8 shows the value of each cash flow and the total present value. The annuity formula, however, is generally quicker; you simply need to multiply the $5,000 cash flow by the annuity factor:
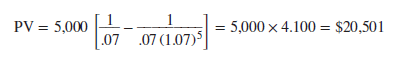
3. Valuing Annuities Due
When we costed the installment plan we assumed that the first payment was made at the end of the year. Suppose instead that the first of the five yearly payments is due immediately. How does this change the cost of the car?
If we discount each cash flow by one less year, the present value is increased by the multiple (1 + r). In the case of the car purchase the present value of the payments becomes 20,501 X (1 + r) = 20,501 X 1.07 = $21,936.
A level stream of payments starting immediately is called an annuity due. An annuity due is worth (1 + r) times the value of an ordinary annuity.
4. Calculating Annual Payments
Annuity problems can be confusing on first acquaintance, but you will find that with practice they are generally straightforward. For example, here is a case where you need to use the annuity formula to find the amount of the payment given the present value.
Example 2.3 • Paying Off a Bank Loan
Bank loans are paid off in equal installments. Suppose that you take out a four-year loan of $1,000. The bank requires you to repay the loan evenly over the four years. It must therefore set the four annual payments so that they have a present value of $1,000. Thus,
PV = annual loan payment X 4-year annuity factor = $1,000
Annual loan payment = $1,000/4-year annuity factor
Suppose that the interest rate is 10% a year. Then

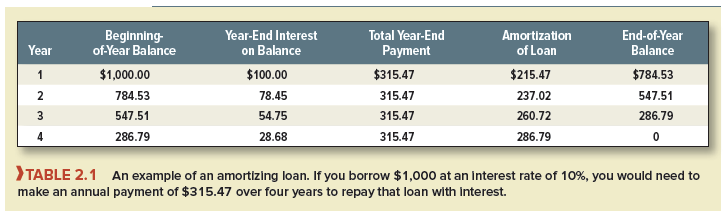
Let’s check that this annual payment is sufficient to repay the loan. Table 2.1 provides the calculations. At the end of the first year, the interest charge is 10% of $1,000, or $100. So $100 of the first payment is absorbed by interest, and the remaining $215.47 is used to reduce the loan balance to $784.53.
Next year, the outstanding balance is lower, so the interest charge is only $78.45. Therefore $315.47 – $78.45 = $237.02 can be applied to paying off the loan. Because the loan is progressively paid off, the fraction of each payment devoted to interest steadily falls over time, while the fraction used to reduce the loan increases. By the end of year 4, the amortization is just enough to reduce the balance of the loan to zero.
Loans that involve a series of level payments are known as amortizing loans. “Amortizing” means that part of the regular payment is used to pay interest on the loan and part is used to pay off or amortize the loan.
Example 2.4 • Calculating Mortgage Payments
Most mortgages are amortizing loans. For example, suppose that you take out a $250,000 house mortgage from your local savings bank when the interest rate is 12%. The bank requires you to repay the mortgage in equal annual installments over the next 30 years.
Thus,
Annual mortgage payment = $250,000/30-year annuity factor
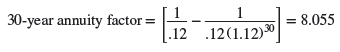
and
Annual mortgage payment = 250,000/8.055 = $31,036
Figure 2.9 shows that in the early years, almost all of the mortgage payment is eaten up by interest and only a small fraction is used to reduce the amount of the loan. Even after 15 years, the bulk of the annual payment goes to pay the interest on the loan. From then on, the amount of the loan begins to decline rapidly.

Excellent post. I was checking continuously this blog and I am impressed! Extremely helpful info specifically the last part 🙂 I care for such info much. I was seeking this particular info for a long time. Thank you and best of luck.