Production with Two Outputs—Economies of Scope

Many firms produce more than one product. Sometimes a firm’s products are closely linked to one another: A chicken farm, for instance, produces poultry and eggs, an automobile company produces automobiles and trucks, and a uni- versity produces teaching and research. At other times, firms produce physically unrelated products. In both cases, however, a firm is likely to enjoy production or cost advantages when it produces two or more products. These advantages could result from the joint use of inputs or production facilities, joint marketing programs, or possibly the cost savings of a common administration. In some cases, the production of one product yields an automatic and unavoidable by- product that is valuable to the firm. For example, sheet metal manufacturers produce scrap metal and shavings that they can sell.

1. Product Transformation  Curves

To study the economic advantages of joint production, let’s consider an automo- bile company that produces two products, cars and tractors. Both products use capital (factories and machinery) and labor as inputs. Cars and tractors are not typically produced at the same plant, but they do share management resources, and both rely on similar machinery and skilled labor. The managers of the com- pany must choose how much of each product to produce. Figure 7.11 shows two product transformation curves, each showing the various combinations of cars and tractors that can be produced with a given input of labor and machinery. Curve O1  describes all combinations of the two outputs that can be produced

with a relatively low level of inputs, and curve O2 describes the output combina-tions associated with twice the inputs. Why does the product transformation curve have a negative slope? Because in order to get more of one output, the firm must give up some of the other output. For example, a firm that emphasizes car production will devote less of its resources to producing tractors. In Figure 7.11, curve O2 lies twice as far from the origin as curve O1, signifying that this firm’s production process exhibits constant returns to scale in the production of both commodities.

If curve 0₁ were a straight line, joint production would entail no gains (or losses). One smaller company specializing in cars and another in tractors would generate the same output as a single company producing both. However, the product transformation curve is bowed outward (or concave) because joint pro­duction usually has advantages that enable a single company to produce more cars and tractors with the same resources than would two companies producing each product separately. These production advantages involve the joint sharing of inputs. A single management, for example, is often able to schedule and orga­nize production and to handle accounting and financial activities more effec­tively than separate managements.

2. Economies and Diseconomies of Scope

In general, economies of scope are present when the joint output of a single firm is greater than the output that could be achieved by two different firms each producing a single product (with equivalent production inputs allocated between them). If a firm’s joint output is less than that which could be achieved by separate firms, then its production process involves diseconomies of scope. This possibility could occur if the production of one product somehow con- flicted with the production of the second.

There is no direct relationship between economies of scale and economies of scope. A two-output firm can enjoy economies of scope even if its production pro- cess involves diseconomies of scale. Suppose, for example, that manufacturing flutes and piccolos jointly is cheaper than producing both separately. Yet the production process involves highly skilled labor and is most effective if undertaken on a small scale. Likewise, a joint-product firm can have economies of scale for each individual product yet not enjoy economies of scope. Imagine, for example, a large conglomer- ate that owns several firms that produce efficiently on a large scale but that do not take advantage of economies of scope because they are administered separately.

3. The Degree of Economies of Scope

The extent to which there are economies of scope can also be determined by studying a firm’s costs. If a combination of inputs used by one firm generates more output than two independent firms would produce, then it costs less

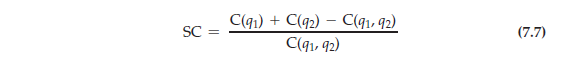
C(q₁) represents the cost of producing only output q₁, C(q₂) represents the cost of producing only output q₂, and C(q₁, q₂) the joint cost of producing both outputs. When the physical units of output can be added, as in the car-tractor example, the expression becomes C(qi + q₂). With economies of scope, the joint cost is less than the sum of the individual costs. Thus, SC is greater than 0. With disecono­mies of scope, SC is negative. In general, the larger the value of SC, the greater the economies of scope.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.