The company cost of capital is defined as the expected return on a portfolio of all the company’s outstanding debt and equity securities. It is the opportunity cost of capital for an investment in all of the firm’s assets, and therefore the appropriate discount rate for the firm’s average-risk projects.
If the firm has no debt outstanding, then the company cost of capital is just the expected rate of return on the firm’s stock. Many large, successful companies pretty well fit this special case, including Johnson & Johnson (J&J). The estimated beta of Johnson & Johnson’s common stock is .81. Suppose that the risk-free interest rate is 2% and the market risk premium is 7%. Then the capital asset pricing model would imply an expected return of 7.7% from J&J’s stock:
![]()
If J&J is contemplating an expansion of its existing business, it would make sense to discount the forecasted cash flows at 7.7%.
The company cost of capital is not the correct discount rate if the new projects are more or less risky than the firm’s existing business. Each project should, in principle, be evaluated at its own opportunity cost of capital. This is a clear implication of the value-additivity principle introduced in Chapter 7. For a firm composed of assets A and B, the firm value is
Firm value = PV(AB) = PV(A) + PV(B)
= sum of separate asset values
Here, PV(A) and PV(B) are valued just as if they were mini-firms in which stockholders could invest directly. Investors would value A by discounting its forecasted cash flows at a rate reflecting the risk of A. They would value B by discounting at a rate reflecting the risk of B. The two discount rates will, in general, be different. If the present value of an asset depended on the identity of the company that bought it, present values would not add up, and we know they do add up. (Think of a portfolio of $1 million invested in J&J and $1 million invested in Toyota. Would any reasonable investor say that the portfolio is worth anything more or less than $2 million?)
If the firm considers investing in a third project C, it should also value C as if C were a mini-firm. That is, the firm should discount the cash flows of C at the expected rate of return that investors would demand if they could make a separate investment in C. The opportunity cost of capital depends on the use to which that capital is put.
Perhaps we’re saying the obvious. Think of J&J: It is a massive health care and consumer products company, with $76 billion in sales in 2017. J&J has well-established consumer products, including Band-Aid® bandages, Tylenol®, and products for skin care and babies. It also invests heavily in much chancier ventures, such as biotech research and development (R&D). Do you think that a new production line for baby lotion has the same cost of capital as an investment in biotech R&D? We don’t, though we admit that estimating the cost of capital for biotech R&D could be challenging.
Suppose we measure the risk of each project by its beta. Then J&J should accept any project lying above the upward-sloping security market line that links expected return to risk in Figure 9.1. If the project is high risk, J&J needs a higher prospective return than if the project is low risk. That is not the same as accepting any project regardless of its risk as long as it offers a higher return than the company’s cost of capital. In that case, J&J would accept any project above the horizontal cost of capital line in Figure 9.1—that is, any project offering a return of more than 7.7%.
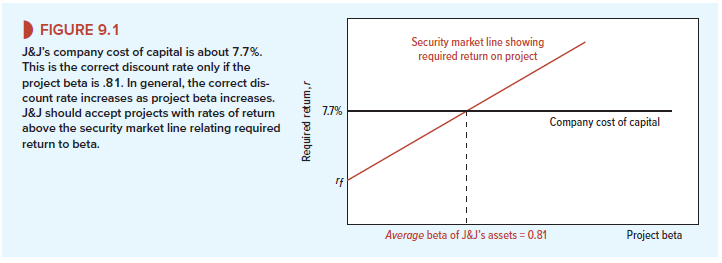
It is clearly silly to suggest that J&J should demand the same rate of return from a very safe project as from a very risky one. If J&J used the company cost of capital rule, it would reject many good low-risk projects and accept many poor high-risk projects. It is also silly to suggest that just because another company has a still lower company cost of capital, it is justified in accepting projects that J&J would reject.
1. Perfect Pitch and the Cost of Capital
The true cost of capital depends on project risk, not on the company undertaking the project. So why is so much time spent estimating the company cost of capital?
There are two reasons. First, many (maybe most) projects can be treated as average risk— that is, neither more nor less risky than the average of the company’s other assets. For these projects the company cost of capital is the right discount rate. Second, the company cost of capital is a useful starting point for setting discount rates for unusually risky or safe projects. It is easier to add to, or subtract from, the company cost of capital than to estimate each project’s cost of capital from scratch.
There is a good musical analogy here. Most of us, lacking perfect pitch, need a well-defined reference point, like middle C, before we can sing on key. But anyone who can carry a tune gets relative pitches right. Businesspeople have good intuition about relative risks, at least in industries they are used to, but not about absolute risk or required rates of return. Therefore, they set a company-wide cost of capital as a benchmark. This is not the right discount rate for everything the company does, but adjustments can be made for more or less risky ventures.
That said, we have to admit that many large companies use the company cost of capital not just as a benchmark, but also as an all-purpose discount rate for every project proposal. Measuring differences in risk is difficult to do objectively, and financial managers shy away from intracorporate squabbles. (You can imagine the bickering: “My projects are safer than yours! I want a lower discount rate!” “No they’re not! Your projects are riskier than a naked call option!”)[2]
When firms force the use of a single company cost of capital, risk adjustment shifts from the discount rate to project cash flows. Top management may demand extra-conservative cash-flow forecasts from extra-risky projects. Or they may refuse to sign off on an extra-risky project unless NPV, computed at the company cost of capital, is well above zero. Such rough- and-ready risk adjustments may be better than none at all.
2. Debt and the Company Cost of Capital
We defined the company cost of capital as “the expected return on a portfolio of all the company’s outstanding debt and equity securities.” Thus, the cost of capital is estimated as a blend of the cost of debt (the interest rate on the firm’s debt) and the cost of equity (the expected rate of return demanded by investors in the firm’s common stock).
Suppose the company’s market-value balance sheet looks like this:

The values of debt and equity add up to overall firm value (D + E = V) and firm value V equals asset value. These figures are all market values, not book (accounting) values. The market value of equity is often much larger than the book value, so the market debt ratio D/V is often much lower than a debt ratio computed from the book balance sheet.
The 7.5% cost of debt is the opportunity cost of capital for the investors who hold the firm’s debt. The 15% cost of equity is the opportunity cost of capital for the investors who hold the firm’s shares. Neither measures the company cost of capital, that is, the opportunity cost of investing in the firm’s assets. The cost of debt is less than the company cost of capital, because debt is safer than the assets. The cost of equity is greater than the company cost of capital, because the equity of a firm that borrows is riskier than the assets. Equity is not a direct claim on the firm’s free cash flow. It is a residual claim that stands behind debt.
The company cost of capital is not equal to the cost of debt or to the cost of equity but is a blend of the two. Suppose you purchased a portfolio consisting of 100% of the firm’s debt and 100% of its equity. Then you would own 100% of its assets lock, stock, and barrel. You would not share the firm’s free cash flow with anyone; every dollar that the firm pays out would be paid to you.
The expected rate of return on your hypothetical portfolio is the company cost of capital. The expected rate of return is just a weighted average of the cost of debt (rD = 7.5%) and the cost of equity (rE = 15%). The weights are the relative market values of the firm’s debt and equity, that is, D/V = 30% and E/V = 70%.
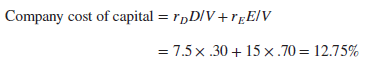
This blended measure of the company cost of capital is called the weighted-average cost of capital or WACC (pronounced “whack”). Calculating WACC is a bit more complicated than our example suggests, however. For example, interest is a tax-deductible expense for
corporations, so the after-tax cost of debt is (1 – Tc)rD, where Tc is the marginal corporate tax rate. Suppose Tc = 21%, its rate in the United States in 2018. Then after-tax WACC is
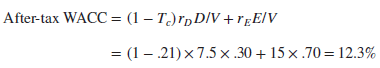
We give another example of the after-tax WACC later in this chapter, and we cover the topic in much more detail in Chapter 19. But now, we turn to the hardest part of calculating WACC, estimating the cost of equity.

23 Jun 2021
24 Jun 2021
24 Jun 2021
25 Jun 2021
25 Jun 2021
25 Jun 2021