Permutations and Combinations

After doing sampling, the result of which is the set of a smaller number of elements, the relevant questions are

1. In how many different ways can we arrange the given (small) number of elements of the set, deal­ing with all of them together?
2. How many different subsets can we form out of a given set of elements, conforming to certain speci­fied constraints?

These questions lead us to what are known as permutations and combinations in a set.

With the prospect of having to deal with experiments that have many causes acting together, it is necessary to know the per­mutations and combinations possible within a set of a given number of things, objects or otherwise. Any arrangement of a group or set of specific things in a specified order (AB is different from BA) is a permutation, whereas a group or set of specific things, disregarding order, is a combination (AB = BA).

1. Permutations

Consider a set of three books, marked A, B, and C, to be placed in a rack that has room for only two of these. The permutation of these three books, two books taken at a time, are six in number:

Further, consider a set of four books, marked A, B, C, and D. Permutations of these when three books are to be taken at a time are twenty-four in number:

The number of permutations can be rationalized without hav­ing to write them as above. We take a close look at the first case: three books, taken two at a time. In the first position, any one of the three books can be placed, meaning that there are three choices. In the second (and only) position left, any one of the remaining two books can be placed, meaning that there are two
choices. Together there are 3 x 2 = 6 possibilities, or permuta­tions. Considering the second case, where there are four books, three of these taken at a time, for the first position, there are four choices, for the second position there are three choices, for the third position (and only one left), there are two choices, together amounting to 4 x 3 x 2 = 24 permutations. We note that this is a product of three factors, consecutive numbers, starting with four.

Along similar lines, the number of possible permutations within a set of n things, taking r things at a time, is

n x (n — 1) x (n — 2) . . . (rth factor)

The third factor above is (n — 2), the fourth factor will be (n — 3), and the fifth factor will be (n — 4). The rth factor will be

n — (r — 1)

= (n — r + 1)

Now, using the designation ⁿP_r for the number of permuta­tions of n things, r of these taken at a time, we may write

ⁿP_r = n(n—1) x (n — 2) . . . x (n — r + 1)                          (16.1)

If, in the set of n things, all of them are taken at a time (r = n), we have

ⁿP_n = n x (n — 1) x (n — 2) . . . x 3 x 2 x 1                        (16.2)

The product of all rational numbers from n to 1 is called the factorial of n and is symbolized as n!

Then

Using this symbol, further simplification of (16.1) is possible; multiplying and dividing by the same factor shown in square brackets below, we have

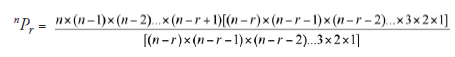
In this, we note that the denominator is (n — r)!, and the numerator is n! Therefore,

2. Combinations

Combinations of three things, A, B, C, with two of these taken at a time, are

AB                   BC                  CA

The other three

BA             CB                  AC

do not count as combinations, because these are only variations in order. In the second case we considered, with four things, A, B, C, D, three of these taken at a time, the combinations are

ABC    BCD   CDA   DAB

The six variations in each column headed by those, in the group of twenty-four numbers shown earlier, are simply the per­mutations possible with three things, all of them taken at a time; hence, the number of these is 3! Thus, the number of combina­tions possible with four things, three of these taken at a time, des­ignated as ⁴C3, is related to the corresponding permutation as

Generalizing along the same lines as above, we may write the number of combinations possible within a set of n things, taking r things at a time, as

ⁿP_r = ⁿC_r r!                                                                                (16.5)

from which we get

ⁿC_r = ⁿP_r + r!                                                                             (16.6)

Further, substituting for ⁿP_r from (16.4), we obtain expression for

Source: Srinagesh K (2005), The Principles of Experimental Research, Butterworth-Heinemann; 1st edition.