Shifts and Role of Six Sigma

Six Sigma promotes the idea that the distribution of output for a stable, normally distributed process (voice of the process) should be designed to take up no more than half of the tolerance allowed by the specification limits (voice of the customer). Although processes may be designed to be at their best, it is assumed that over time the variation may increase. This increase in variation may be due to small variations in process inputs, the way the process is monitored, changing conditions, etc. The increase in process variation is often assumed for sake of descriptive simplicity to be similar to temporary shifts in the underlying process mean. The increase in process variation has been shown in practice to be equivalent to an average shift of 1.5 standard deviations in the mean of the originally designed and monitored process. If a process is originally designed to be twice as good as a customer demands (i.e., the specifications representing the customer requirements are six standard deviations from the process target), then even with a shift in the distribution of output the customer demands are likely to be met. In fact, even if the process shifts off target by 1.5 standard deviations, there are 4.5 standard deviations between the process mean (m + 1.50c) and its closest specification ( m + 6.00 c). This results in, at worst 3.4 defects per million opportunities (DPMO) at the time the process has shifted or the variation has increased to have similar impact as a 1.5 standard deviation shift.

The characteristics of a process can be categorized as variables and attributes. For each process, the desired value of a characteristic is specified as its mean value. The allowed range of variation of the variable is specified as the tolerance range (or specification width) and is set by the lower specification limit (LSL) and the upper specification limit (USL).

1.  Unshifted Processes

If the LSL and the USL are placed symmetrically around the mean value and the mean of a process variable equals the (desired) nominal or mean value, the process is called a centered process or an unshifted process.

2. Three Sigma Process with a 0.0 Shift in the Mean

Figure 7.1 shows the “voice of the process” for an accounting function with an average of seven days, a standard deviation of one day and a stable normal distribution. It also shows a nominal value of seven days, a lower specification limit of four days and an upper specifica­tion limit of ten days. The accounting function is referred to as a Three Sigma process because the process mean plus or minus three standard deviations is equal to the specification limits. In other terms, USL = m + 3sand LSL = m – 3s. This scenario will yield 2,700 defects per million opportunities or one early or late monthly report in 30.86 years [(1/0.0027)/12].

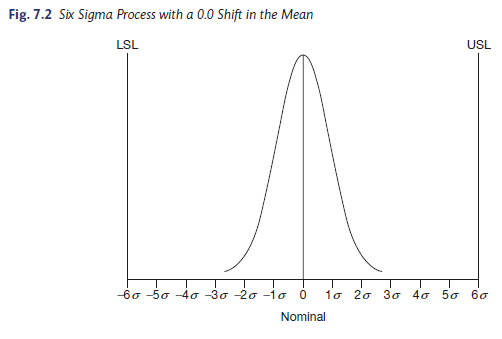
3. Six Sigma Process with a 0.0 Shift in the Mean

Figure 7.2 shows the same scenario as Figure 7.1 except the “voice of the process” only takes half the distance between the specification limits. The process mean remains the same as in Figure 7.1, but the process standard deviation has been reduced to one half-day through application of the DMAIC model. In this case, the resulting output will exhibit 2 defects per billion opportunities or one early or late monthly report in 41,666,667 years [(1/0.000000002)/12].

4. Shifted Processes

It is difficult in a real process environment to control a process in a manner that the mean exactly hits the nominal target mean. Therefore, a shift in the process has to be allowed for. Motorola’s Six Sigma quality level allows an off-centering of the process up to 1.5 Sigma.

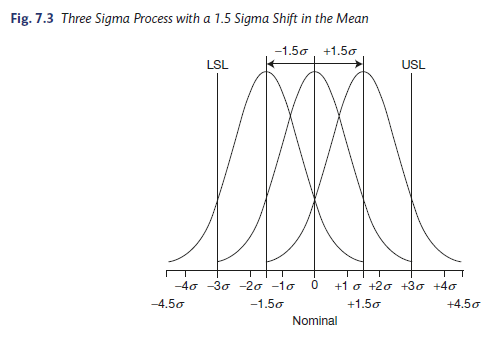
5. Three Sigma Process with a 1.5 Sigma Shift in the Mean

Figure 7.3 shows the same scenario as Figure 7.1, but the process mean shifts by 1.5 standard deviations (the process average is shifted up or down by 1.5 standard deviations [or 1.5 days] from 7 days to5.5 days or 8.5 days) over time. This is not an uncommon phenomenon. The 1.5 standard deviation shift in the mean results in 66,807 defects per million opportunities at the nearest specification limit, or one early or late monthly report in 1.25 years [(1/0.066807)/12].

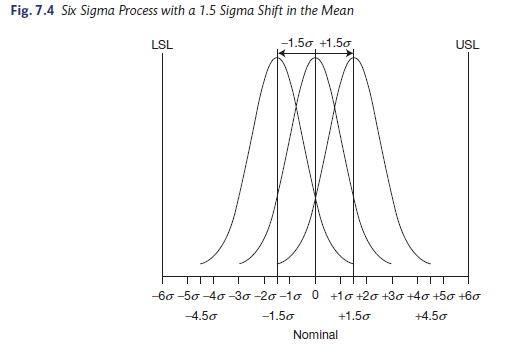
6. Six Sigma Process with a 1.5 Sigma Shift in the Mean

Figure 7.4 shows the same scenario as Figure 7.3, but the process average shifts by 1.5 stan­dard deviations (the process average is shifted up or down by 1.5 standard deviations [or 0.75 days = 1.5 x 0.5 days] from 7.0 days to 6.25 days or 7.75 days) over time. The 1.5 standard deviation shift in the mean results in 3.4 defects per million opportunities or one early or late monthly report in 24,510 years [(1/0.0000034/12]. This is the definition of Six Sigma level of quality.

Motorola’s Six Sigma quality level allows an off-centering of the process upto 1.5 Sigma. The Six Sigma quality level is measured in terms of defectives per million opportunities (DPMO).

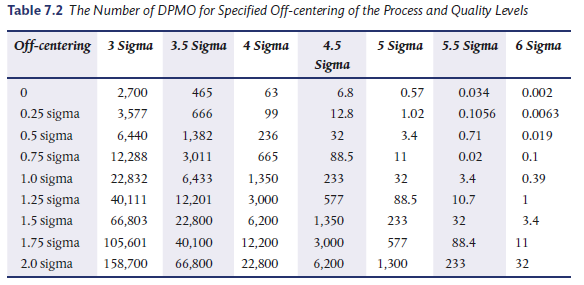
Table 7.2 shows the number of defective parts per million opportunities for speci­fied off-centering of the process and quality levels. Note that in the table the first row shows the DPMO when there is no off-centering of the process. At Three Sigma qual­ity level, it shows the DPMO as 2,700, while at Six Sigma quality level the DPMO is 0.002, i.e. 2 defects per billion. For an off-centering of 1.5 Sigma and Sigma quality level, the DPMO is shown as 3.4. Thus, Motorola has quality levels such that 3.4 defects per million are allowed. For a process without off-centering, 3.4 defects per million lie somewhere between 4.5 and 5 Sigma quality levels. For zero off-centering, the 4.5 Sigma quality level has a DPMO of 6.8, while 5 Sigma quality level has a DPMO of 0.57. Thus, the DPMO of 3.4 lies in between DPMO of 0.57 and 6.8, i.e. between 4.5 and 5 Sigma quality levels without off-centering.

Source: Poornima M. Charantimath (2017), Total Quality Management, Pearson; 3rd edition.