We have seen that owners and managers of firms can have asymmetric information about demand, cost, and other variables. We’ve also seen how owners can design reward structures to encourage managers to make appropriate efforts. Now we focus our attention on firms that are integrated—that consist of several divisions, each with its own managers. Some firms are horizontally integrated: Several plants produce the same or related products. Others are also vertically integrated: Upstream divisions produce materials, parts, and components that downstream divisions use to produce final products. Integration creates organizational problems. We addressed some of these problems in the appendix to Chapter 11, where we discussed transfer pricing in the vertically integrated firm—that is, how the firm sets prices for parts and components that upstream divisions supply to downstream divisions. Here we will examine problems that stem from asymmetric information.
1. Asymmetric Information and Incentive Design in the Integrated Firm
In an integrated firm, division managers are likely to have better information about their different operating costs and production potential than central management has. This asymmetric information causes two problems.
- How can central management elicit accurate information about divisional operating costs and production potential from divisional managers? This information is important because the inputs into some divisions may be the outputs of other divisions, because deliveries must be scheduled to customers, and because prices cannot be set without knowing overall production capacity and costs.
- What reward or incentive structure should central management use to encourage divisional managers to produce as efficiently as possible? Should they be given bonuses based on how much they produce? If so, how should they be structured?
To understand these problems, consider a firm with several plants that all produce the same product. Each plant’s manager has much better information about its production capacity than central management has. In order to avoid bottlenecks and to schedule deliveries reliably, central management wants to learn more about how much each plant can produce. It also wants each plant to produce as much as possible. Let’s examine ways in which central management can obtain the information it wants while also encouraging plant managers to run the plants as efficiently as possible.
One way is to give plant managers bonuses based on either the total output of their plant or its operating profit. Although this approach would encourage managers to maximize output, it would penalize managers whose plants have higher costs and lower capacity. Even if these plants produced efficiently, their output and operating profit—and thus their bonuses—would be lower than those of plants with lower costs and higher capacities. Plant managers would also have no incentive to obtain and reveal accurate information about cost and capacity.
A second way is to ask managers about their costs and capacities and then base bonuses on how well they do relative to their answers. For example, each manager might be asked how much his or her plant can produce each year. Then at the end of the year, the manager receives a bonus based on how close the plant’s output was to this target. For example, if the manager’s estimate of the feasible production level is Q, the annual bonus in dollars, B, might be
B = 10,000 – .5(Qf – Q) (17.3)
where Q is the plant’s actual output, 10,000 is the bonus when output is at capacity, and .5 is a factor chosen to reduce the bonus if Q is below Qf.
Under this scheme, however, managers would have an incentive to underestimate capacity. By claiming capacities below what they know to be true, they can more easily earn large bonuses even if they do not operate efficiently. For example, if a manager estimates capacity to be 18,000 rather than 20,000, and the plant actually produces only 16,000, her bonus increases from $8000 to $9000. Thus this scheme fails to elicit accurate information about capacity and does not ensure that plants will be run as efficiently as possible.
Now let’s modify this scheme. We will still ask managers how much their plants can feasibly produce and tie their bonuses to this estimate. However, we will use a slightly more complicated formula than the one in (17.3) to calculate the bonus:
If Q > Qf, B = 3Qf + .2(Q – Q)
If Q < Qf, B = .3Qf – .5(Qf – Q)
The parameters (.3, .2, and .5) have been chosen so that each manager has the incentive to reveal the true feasible production level and to make Q, the actual output of the plant, as large as possible.
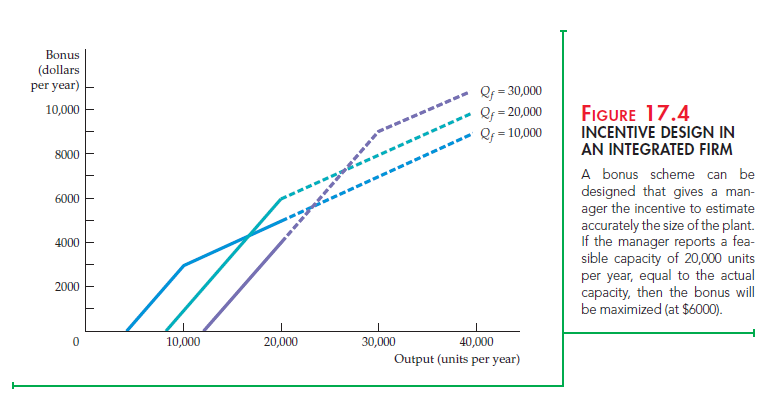
To see that this scheme does the job, look at Figure 17.4. Assume that the true production limit is Q* = 20,000 units per year. The bonus that the manager will receive if she states feasible capacity to be the true production limit is given by the line labeled Qf = 20,000. This line is continued for outputs beyond 20,000 to illustrate the bonus scheme but dashed to signify the infeasibility of such production. Note that the manager’s bonus is maximized when the firm produces at its limits of 20,000 units; the bonus is then $6000.
Suppose, however, that the manager reports a feasible capacity of only 10,000. Then the bonus is given by the line labeled Qf = 10,000. The maximum bonus is now $5000, which is obtained by producing an output of 20,000. But note that this is less than the bonus that the manager would receive if she correctly stated the feasible capacity to be 20,000.
The same line of argument applies when the manager exaggerates available capacity. If the manager states feasible capacity to be 30,000 units per year, the bonus is given by the line Qf = 30,000. The maximum bonus of $4000, which is achieved at an output of 20,000, is less than the bonus that she could have received by reporting feasible capacity correctly.
2. Applications
Because the problem of asymmetric information and incentive design comes up often in managerial settings, incentive schemes like the one described above arise in many contexts. How, for example, can managers encourage salespeople to set and reveal realistic sales targets and then work as hard as possible to meet them?
Most salespeople cover specific territories. A salesperson assigned to a densely populated urban territory can usually sell more product than a salesperson assigned to a sparsely populated area. The company, however, wants to reward all salespeople equitably. It also wants to give them the incentive to work as hard as possible and to report realistic sales targets, so that it can plan production and delivery schedules. Companies have always used bonuses and commissions to reward salespeople, but incentive schemes have often been poorly designed. Typically, salespeople’s commissions were proportional to their sales. This approach elicited neither accurate information about feasible sales targets nor maximum performance.
Today, companies are learning that bonus schemes like the one given by equation (17.4) provide better results. The salesperson can be given an array of numbers showing the bonus as a function of both the sales target (chosen by the salesperson) and the actual level of sales. (The numbers would be calculated from equation (17.4) or some similar formula.) Salespeople will quickly figure out that they do best by reporting feasible sales targets and then working as hard as possible to meet them.
Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.

Very superb info can be found on web blog.