Simple Linear Regression Model Assumptions

In conducting a regression analysis, we begin by making an assumption about the appropri­ate model for the relationship between the dependent and independent variable(s). For the case of simple linear regression, the assumed regression model is

Then the least squares method is used to develop values for β₀ and β₁, the estimates of the model parameters β₀ and β₁, respectively. The resulting estimated regression equation is

We saw that the value of the coefficient of determination (r²) is a measure of the goodness of fit of the estimated regression equation. However, even with a large value of r², the estimated regression equation should not be used until further analysis of the appropriateness of the assumed model has been conducted. An important step in determining whether the assumed model is appropriate involves testing for the signific­ance of the relationship. The tests of significance in regression analysis are based on the following assumptions about the error term ∈.

Figure 14.6 illustrates the model assumptions and their implications; note that in this graphical interpretation, the value of E(y) changes according to the specific value of x con­sidered. However, regardless of the x value, the probability distribution of e and hence the probability distributions of y are normally distributed, each with the same variance. The specific value of the error e at any particular point depends on whether the actual value of y is greater than or less than E(y).

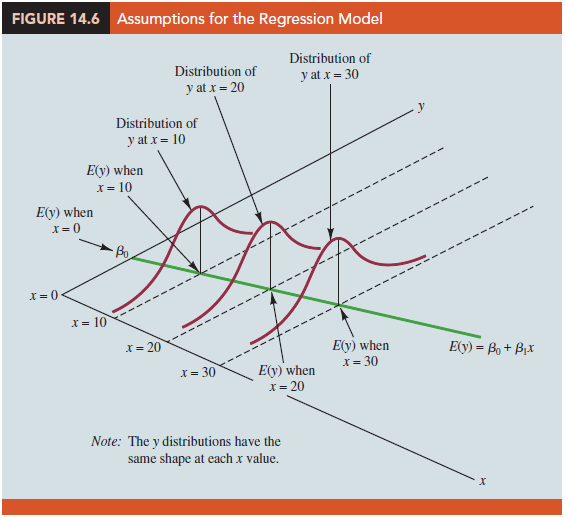
At this point, we must keep in mind that we are also making an assumption or hypothe­sis about the form of the relationship between x and y. That is, we assume that a straight line represented by β₀ + β₁x is the basis for the relationship between the variables. We must not lose sight of the fact that some other model, for instance y = β₀ + β₁x² + ∈, may turn out to be a better model for the underlying relationship.

Source:  Anderson David R., Sweeney Dennis J., Williams Thomas A. (2019), Statistics for Business & Economics, Cengage Learning; 14th edition.