Advertising

We have seen how firms can utilize their market power when making pricing decisions. Pricing is important for a firm, but most firms with market power have another important decision to make: how much to advertise. In this sec- tion, we will see how firms with market power can make profit-maximizing advertising decisions, and how those decisions depend on the characteristics of demand for the firm’s product.20

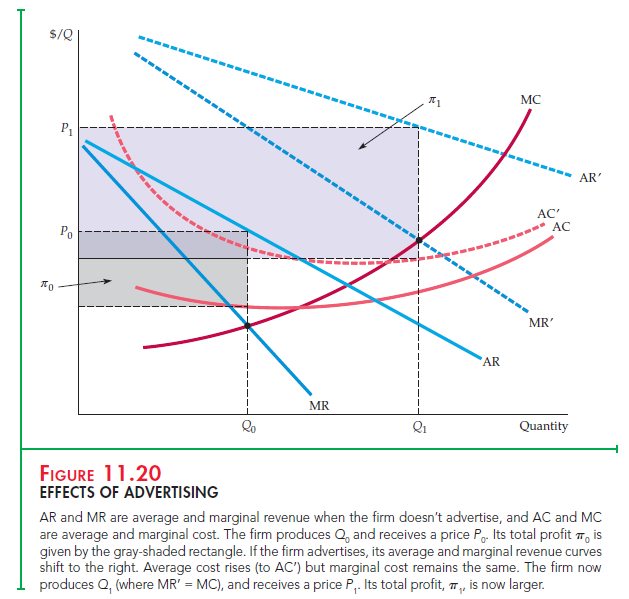
For simplicity, we will assume that the firm sets only one price for its product. We will also assume that having done sufficient market research, it knows how its quantity demanded depends on both its price P and its advertising expendi- tures in dollars A; that is, it knows Q(P, A). Figure 11.20 shows the firm’s demand and cost curves with and without advertising. AR and MR are the firm’s average and marginal revenue curves when it does not advertise, and AC and MC are its average and marginal cost curves. It produces a quantity Q0, where MR = MC, and receives a price P0. Its profit per unit is the difference between P0  and aver-age cost, so its total profit p0 is given by the gray-shaded rectangle.

Now suppose the firm advertises. This causes its demand curve to shift out and to the right; the new average and marginal revenue curves are given by AR’ and MR’. Advertising is a fixed cost, so the firm’s average cost curve rises (to AC’). Marginal cost, however, remains the same. With advertising, the firm produces Q1 (where MR’ = MC) and receives a price P1. Its total profit p1, given by the purple-shaded rectangle, is now much larger.

Although the firm in Figure 11.20 is clearly better off when it advertises, the fig­ure does not help us determine how much advertising it should do. It must choose its price P and advertising expenditure A to maximize profit, which is now given by:

Given a price, more advertising will result in more sales and thus more revenue. But what is the firm’s profit-maximizing advertising expenditure? You might be tempted to say that the firm should increase its advertising expendi­tures until the last dollar of advertising just brings forth an additional dollar of revenue—that is, until the marginal revenue from advertising, A(PQ)/AA, is just equal to 1. But as Figure 11.20 shows, this reasoning omits an important element. Remember that advertising leads to increased output (in the figure, output increased from Q₀ to Q₁). But increased output in turn means increased produc­tion costs, and this must be taken into account when comparing the costs and benefits of an extra dollar of advertising.

The correct decision is to increase advertising until the marginal revenue from an additional dollar of advertising, MR_Ads, just equals the full marginal cost of that advertising. That full marginal cost is the sum of the dollar spent directly on the advertising and the marginal production cost resulting from the increased sales that advertising brings about. Thus the firm should advertise up to the point that

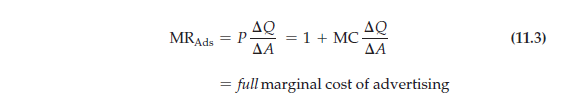
This rule is often ignored by managers, who justify advertising budgets by com­paring the expected benefits (i.e., added sales) only with the cost of the adver­tising. But additional sales mean increased production costs that must also be taken into account.

A Rule of Thumb for Advertising

Like the rule MR = MC, equation (11.3) is sometimes difficult to apply in practice. In Chapter 10, we saw that MR = MC implies the following rule of thumb for pricing: (P – MC)/P = -1/E_D, where E_D is the firm’s price elasticity of demand. We can combine this rule of thumb for pricing with equation (11.3) to obtain a rule of thumb for advertising.

First, rewrite equation (11.3) as follows:

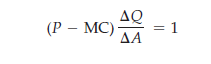
Now multiply both sides of this equation by A/PQ, the advertising-to-sales ratio:

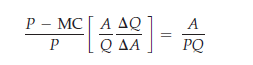
The term in brackets, (A/Q)( A Q/A A), is the advertising elasticity of demand, the percentage change in the quantity demanded that results from a 1-percent increase in advertising expenditures. We will denote this elasticity by E_A. Because (P – MC)/P must equal -1/E_p, we can rewrite this equation as follows:

Equation (11.4) is a rule of thumb for advertising. It says that to maximize profit, the firm’s advertising-to-sales ratio should be equal to minus the ratio of the advertising and price elasticities of demand. Given information (from, say, market research studies) on these two elasticities, the firm can use this rule to check that its advertising budget is not too small or too large.

To put this rule into perspective, assume that a firm is generating sales rev- enue of $1 million per year while allocating only $10,000 (1 percent of its rev- enues) to advertising. The firm knows that its advertising elasticity of demand is .2, so that a doubling of its advertising budget from $10,000 to $20,000 should increase sales by 20 percent. The firm also knows that the price elasticity of demand for its product is −4. Should it increase its advertising budget, know- ing that with a price elasticity of demand of −4, its markup of price over mar- ginal cost is substantial? The answer is yes; equation (11.4) tells us that the firm’s advertising-to-sales ratio should be −(.2/−4) = 5 percent, so the firm should increase its advertising budget from $10,000 to $50,000.

This rule makes intuitive sense. It says firms should advertise a lot if (i) demand is very sensitive to advertising (EA is large), or if (ii) demand is not very price elastic (EP  is small). Although (i) is obvious, why should firms advertise more when the price elasticity of demand is small? A small elasticity of demand implies a large markup of price over marginal cost. Therefore, the marginal profit from each extra unit sold is high. In this case, if advertising can help sell a few more units, it will be worth its cost.

Source: Pindyck Robert, Rubinfeld Daniel (2012), Microeconomics, Pearson, 8th edition.