Debt financing has one important advantage under the corporate income tax system in the United States and many other countries. The interest that the company pays is a tax-deductible expense. Thus, the return to bondholders escapes taxation at the corporate level.
There is one restriction on this tax benefit. Since 2018, the net amount of interest that companies can deduct is limited to 30% of taxable earnings before interest, taxes, depreciation, and amortization (EBITDA). From 2022 on, this restriction is tightened to 30% of taxable EBIT. (EBIT is, of course, smaller than EBITDA, so less interest can be deducted.[1])
Most large corporations’ interest payments will not hit this constraint, but a few will, with painful results. For example, Dell Technologies carried $52.5 billion of debt at the end of 2017, most as a result of its $67 billion acquisition of EMC in 2016. The company estimated that it would have to pay $200 million per year in extra taxes because of limits on interest deductions. Dell can carry forward unused interest deductions and use them later, if and when the 30% constraint is no longer binding. But the longer the delay, the less the interest tax shields are worth. We predict that Dell will find ways of paying down its debt faster than it would have absent the 30% constraint.
For now, we will assume that the constraint on interest deductions as a percentage of EBITDA or EBIT is not binding. The constraint will merit more thought later in this chapter, however, and also in Chapters 19 and 32.
Table 18.2 shows simple income statements for firm U, which has no debt, and firm L, which has borrowed $1,000 at 8%. L’s tax bill is $17 less than U’s. This is the tax shield provided by the debt of L. In effect the government pays 21% of the interest expense of L. The total income that L can pay out to its bondholders and stockholders increases by that amount.
Tax shields can be valuable assets. Suppose that the debt of L is fixed and permanent. (That is, the company commits to refinance its present debt obligations when they mature and to keep rolling over its debt obligations indefinitely.) Then L can look forward to a permanent stream of cash flows of $17 per year. The risk of these flows is likely to be less than the risk of the operating assets of L. The tax shields depend only on the corporate tax rate[2] and on the ability of L to earn enough to cover interest payments. The corporate tax rate has been pretty stable. And the ability of L to earn its interest payments must be reasonably sure; otherwise it could not have borrowed at 8%. Therefore, we should discount the interest tax shields at a relatively low rate.

But what rate? One common assumption is that the risk of the tax shields is the same as that of the interest payments generating them. Thus, we discount at 8%, the expected rate of return demanded by investors who are holding the firm’s debt:
![]()
In effect, the government assumes 21% of the $1,000 debt obligation of L.
Under these assumptions, the present value of the tax shield is independent of the return on the debt rD. It equals the corporate tax rate Tc times the amount borrowed D:
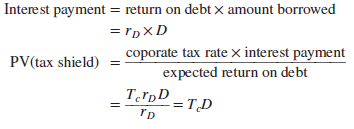
Of course, PV(tax shield) is less if the firm does not plan to borrow a permanent fixed amount,[3] or if it may not have enough taxable income to use the interest tax shields.[4]
1. How Do Interest Tax Shields Contribute to the Value of Stockholders’ Equity?
MM’s proposition 1 amounts to saying that the value of a pie does not depend on how it is sliced. The pie is the firm’s assets, and the slices are the debt and equity claims. If we hold the pie constant, then a dollar more of debt means a dollar less of equity value.
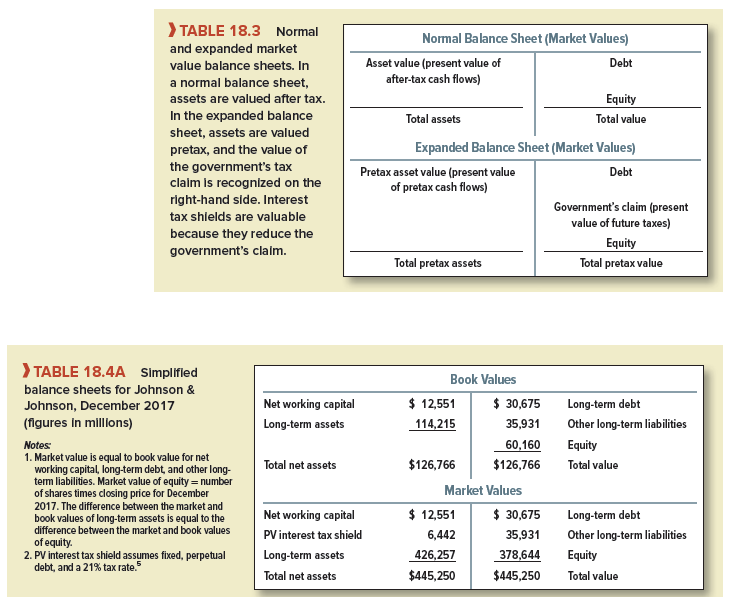
But there is really a third slice, the government’s. Look at Table 18.3. It shows an expanded balance sheet with pretax asset value on the left and the value of the government’s tax claim recognized as a liability on the right. MM would still say that the value of the pie—in this case pretax asset value—is not changed by slicing. But anything the firm can do to reduce the size of the government’s slice obviously makes stockholders better off. One thing it can do is borrow money, which reduces its tax bill and, as we saw in Table 18.2, increases the cash flows to debt and equity investors. The after-tax value of the firm (the sum of its debt and equity values as shown in a normal market value balance sheet) goes up by PV(tax shield).
2. Recasting Johnson & Johnson’s Capital Structure
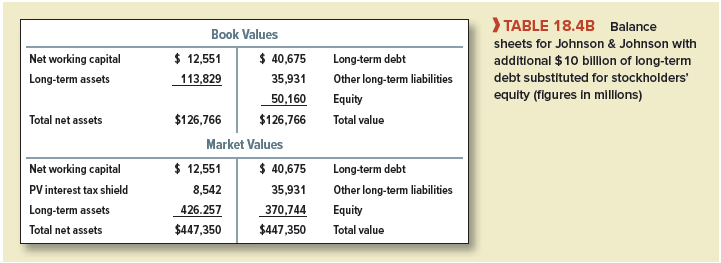
Johnson & Johnson is a large, successful firm that uses relatively little long-term debt. Table 18.4A shows simplified book and market value balance sheets for Johnson & Johnson in December 2017.
Suppose that you were Johnson & Johnson’s financial manager with complete responsibility for its capital structure. You decide to borrow an additional $10 billion on a permanent basis and use the proceeds to repurchase shares.
Table 18.4B shows the new balance sheets. The book version simply has $10,000 million more long-term debt and $10,000 million less equity. But we know that Johnson & Johnson’s assets must be worth more because its tax bill will be reduced by 21% of the interest on the new debt. In other words, Johnson & Johnson has an increase in PV(interest tax shield), which is worth TcD = .21 x $10,000 million = $2,100 million. If the MM theory holds except for taxes, firm value must increase by $2,100 million to $447,350 million. Johnson & Johnson’s equity ends up worth $370,744 million.
Now you have repurchased $10 billion worth of shares, but Johnson & Johnson’s equity value has dropped by only $7.9 billion. Therefore, Johnson & Johnson’s stockholders must be $2.1 billion ahead. Not a bad day’s work.[6]
3. MM and Taxes
We have just developed a version of MM’s proposition 1 as corrected by them to reflect corporate income taxes.[7] The new proposition is
Value of firm = value if all-equity-financed + PV(tax shield)
In the special case of fixed, permanent debt,
![]()
Our imaginary financial surgery on Johnson & Johnson provides the perfect illustration of the problems inherent in this “corrected” theory. That $2.1 billion came too easily; it seems to violate the law that there is no such thing as a money machine. And if Johnson & Johnson’s stockholders would be richer with $40,675 million of corporate debt, why not $50,675 or $60,675 million? At what debt level should Johnson & Johnson stop borrowing? Our formula implies that firm value and stockholders’ wealth continue to go up as D increases. The optimal debt policy appears to be embarrassingly extreme: All firms should be 100% debt-financed.
MM were not that fanatical about it. No one would expect the formula to apply at extreme debt ratios. There are several reasons why our calculations overstate the value of interest tax shields. First, it’s wrong to think of debt as fixed and perpetual; a firm’s ability to carry debt changes over time as profits and firm value fluctuate. Second, some firms face marginal tax rates less than 21%. Third, you can’t use interest tax shields unless there will be future profits to shield—and no firm can be absolutely sure of that. Fourth, the 2017 Tax Cuts and Jobs Act limits the amount of interest that can be deducted to 30% of taxable EBITDA and (after 2021) EBIT. Once a company breaches this limit, additional debt has no further tax advantages over equity.
But none of these qualifications explains why companies like Johnson & Johnson survive and thrive at low debt ratios. It’s hard to believe that its financial managers are simply missing the boat.
We seem to have argued ourselves into a blind alley. But there may be two ways out:
- Perhaps a fuller examination of the U.S. system of corporate and personal taxation will uncover a tax disadvantage of corporate borrowing, offsetting the present value of the interest tax shield.
- Perhaps firms that borrow incur other costs—bankruptcy costs, for example.
We now explore these two escape routes.

This actually answered my downside, thank you!