Multiple regression analysis is the study of how a dependent variable y is related to two or more independent variables. In the general case, we will use p to denote the number of independent variables.
1. Regression Model and Regression Equation
The concepts of a regression model and a regression equation introduced in the preceding chapter are applicable in the multiple regression case. The equation that describes how the dependent variable y is related to the independent variables x1, x2, . . . , xp and an error term is called the multiple regression model. We begin with the assumption that the multiple regression model takes the following form.
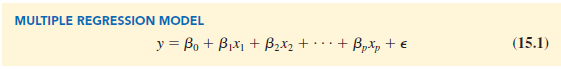
In the multiple regression model, β0, β1, β2, … , βp are the parameters and the error term e (the Greek letter epsilon) is a random variable. A close examination of this model reveals that y is a linear function of x1, x2, . . . , xp (the β0 + β1x1 + ^2 + . . . + βpxp part) plus the error term ∈. The error term accounts for the variability in y that cannot be explained by the linear effect of the p independent variables.
In Section 15.4 we will discuss the assumptions for the multiple regression model and ∈. One of the assumptions is that the mean or expected value of e is zero. A consequence of this assumption is that the mean or expected value of y, denoted E( y), is equal to β0 + β1 x1 + β2x2 + . . . + βpxp. The equation that describes how the mean value of y is related to x1, x2, . . . , xp is called the multiple regression equation.
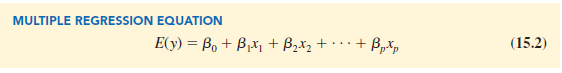
2. Estimated Multiple Regression Equation
If the values of β0, β1, β2, … , βp were known, equation (15.2) could be used to compute the mean value of y at given values of x1, x2, . . . , xp. Unfortunately, these parameter values will not, in general, be known and must be estimated from sample data. A simple random sample is used to compute sample statistics β0, β1, β2,…, βp that are used as the point estimators of the parameters β0, βi, β2, …, βp. These sample statistics provide the following estimated multiple regression equation.


The estimation process for multiple regression is shown in Figure 15.1.
Source: Anderson David R., Sweeney Dennis J., Williams Thomas A. (2019), Statistics for Business & Economics, Cengage Learning; 14th edition.

23 Oct 2019
30 Aug 2021
31 Aug 2021
30 Aug 2021
30 Aug 2021
30 Aug 2021