Variable Selection Procedures

In this section we discuss four variable selection procedures: stepwise regression, for­ward selection, backward elimination, and best-subsets regression. Given a data set with several possible independent variables, we can use these procedures to identify which in­dependent variables provide the best model. The first three procedures are iterative; at each step of the procedure a single independent variable is added or deleted and the new model is evaluated. The process continues until a stopping criterion indicates that the procedure cannot find a better model. The last procedure (best subsets) is not a one-variable-at-a-time procedure; it evaluates regression models involving different subsets of the independent variables.

In the stepwise regression, forward selection, and backward elimination procedures, the criterion for selecting an independent variable to add or delete from the model at each step is based on the F statistic introduced in Section 16.2. Suppose, for instance, that we are considering adding x₂ to a model involving x₁ or deleting x₂ from a model involving x₁ and x₂. To test whether the addition or deletion of x₂ is statistically significant, the null and alternative hypotheses can be stated as follows:

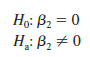
In Section 16.2 (see equation (16.10)) we showed that

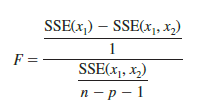
can be used as a criterion for determining whether the presence of x₂ in the model causes a significant reduction in the error sum of squares. The p-value corresponding to this F statistic is the criterion used to determine whether an independent variable should be added or deleted from the regression model. The usual rejection rule applies: Reject H₀ if p-value < a.

1. Stepwise Regression

The stepwise regression procedure begins each step by determining whether any of the variables already in the model should be removed. It does so by first computing an F statistic and a corresponding p-value for each independent variable in the model. The level of significance a for determining whether an independent variable should be removed from the model is referred to as a-to-leave. If the p-value for any inde­pendent variable is greater than a-to-leave, the independent variable with the largest p-value is removed from the model and the stepwise regression procedure begins a new step.

If no independent variable can be removed from the model, the procedure attempts to enter another independent variable into the model. It does so by first computing an F stat­istic and corresponding p-value for each independent variable that is not in the model. The level of significance a for determining whether an independent variable should be entered into the model is referred to as a-to-enter. The independent variable with the smallest p-value is entered into the model provided its p-value is less than or equal to a-to-enter. The procedure continues in this manner until no independent variables can be deleted from or added to the model.

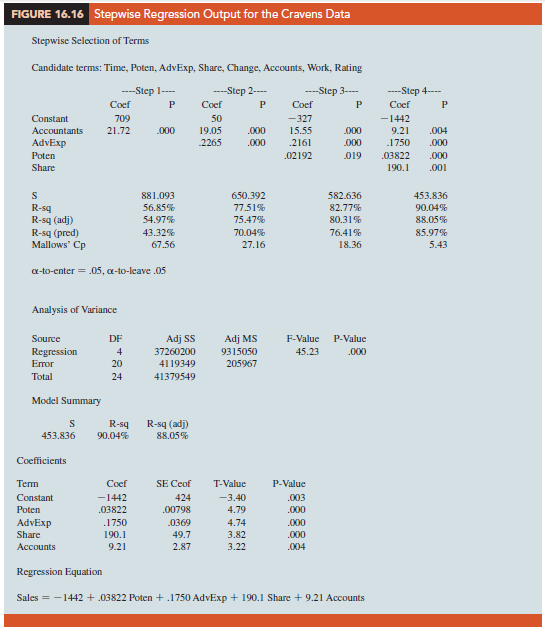
Figure 16.16 shows the results obtained by using the stepwise regression procedure for the Cravens data using values of .05 for a-to-leave and .05 for a-to-enter. The stepwise procedure terminated after four steps. The estimated regression equation identified by the stepwise regression procedure is

Note also in Figure 16.16 that 5 = VMSE has been reduced from 881.093 with the best one-variable model (using Accounts) to 453.836 after four steps. The value of R-sq has been increased from 56.85% to 90.04%, and the recommended estimated regression equa­tion has an R-sq(adj) value of 88.05%.

In summary, at each step of the stepwise regression procedure the first consideration is to see whether any independent variable can be removed from the current model. If none of the independent variables can be removed from the model, the procedure checks to see whether any of the independent variables that are not currently in the model can be entered. Because of the nature of the stepwise regression procedure, an independent variable can enter the model at one step, be removed at a subsequent step, and then enter the model at a later step. The procedure stops when no independent variables can be removed from or entered into the model.

2. Forward Selection

The forward selection procedure starts with no independent variables. It adds variables one at a time using the same procedure as stepwise regression for determining whether an independent variable should be entered into the model. However, the forward selection pro­cedure does not permit a variable to be removed from the model once it has been entered. The procedure stops if the p-value for each of the independent variables not in the model is greater than a-to-enter.

The estimated regression equation obtained using the forward selection procedure is

Thus, for the Cravens data, the forward selection procedure (using .05 for a-to-enter) leads to the same estimated regression equation as the stepwise procedure. However, this will not necessarily be the case for all data sets.

3. Backward Elimination

The backward elimination procedure begins with a model that includes all the independ­ent variables. It then deletes one independent variable at a time using the same procedure as stepwise regression. However, the backward elimination procedure does not permit an independent variable to be reentered once it has been removed. The procedure stops when none of the independent variables in the model has a p-value greater than a-to-leave.

The estimated regression equation obtained using the backward elimination procedure for the Cravens data (using .05 for a-to-leave) is

Comparing the estimated regression equation identified using the backward elimination pro­cedure to the estimated regression equation identified using the forward selection procedure, we see that three independent variables—AdvExp, Poten, and Share—are common to both. However, the backward elimination procedure has included Time instead of Accounts.

Forward selection and backward elimination are the two extremes of model building; the forward selection procedure starts with no independent variables in the model and adds independent variables one at a time, whereas the backward elimination procedure starts with all independent variables in the model and deletes variables one at a time. The two procedures may lead to the same estimated regression equation. It is possible, however, for them to lead to two different estimated regression equations, as we saw with the Cravens data. Deciding which estimated regression equation to use remains a topic for discussion. Ultimately, the analyst’s judgment must be applied. The best-subsets model building pro­cedure we discuss next provides additional model-building information to be considered before a final decision is made.

4. Best-Subsets Regression

Stepwise regression, forward selection, and backward elimination are approaches to choosing the regression model by adding or deleting independent variables one at a time.

None of them guarantees that the best model for a given number of variables will be found. Hence, these one-variable-at-a-time methods are properly viewed as heuristics for selecting a good regression model.

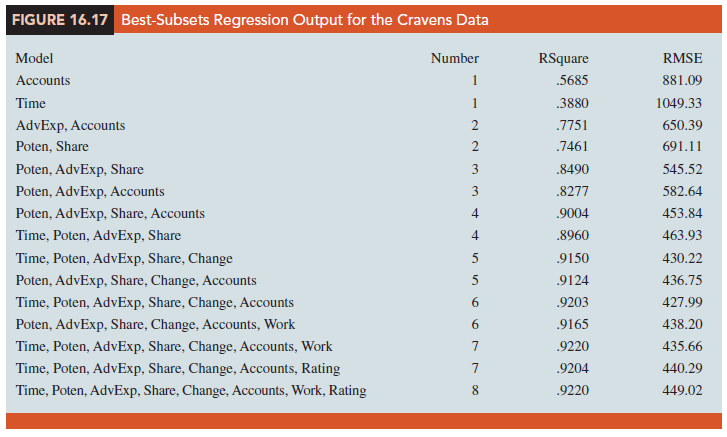
Some software packages use a procedure called best-subsets regression that enables the user to find, given a specified number of independent variables, the best regression model. Figure 16.17 is a portion of the output obtained by using the best-subsets procedure for the Cravens data set.

This output identifies the two best one-variable estimated regression equations, the two best two-variable equations, the two best three-variable equations, and so on. The criterion used in determining which estimated regression equations are best for any number of predictors is the value of the coefficient of determination (R-Sq). For instance, Accounts, with an R-Sq = 56.85%, provides the best estimated regression equation using only one independent variable; AdvExp and Accounts, with an R-Sq = 77.51%, provides the best estimated regression equation using two independent variables; and Poten, AdvExp, and Share, with an R-Sq = 84.90%, provides the best estimated regression equation with three independent variables.

Figure 16.17 also lists the root mean squared error (RMSE) of each of these models, which is computed by taking the square root of the average squared error; a smaller RMSE reflects a model with less squared difference between its predictions and the actual observations. For the Cravens data, the smallest RMSE occurs for the model with the six independent variables: Time, Poten, AdvExp, Share, Change, Accounts, and Work. However, this six-variable model has an R² = 92.03% which is only slightly better than the best model with four independent variables (Poten, AdvExp, Share, and Accounts) which has an R² = 90.04%. All other things being equal, a simpler model with fewer variables is usually preferred.

5. Making the Final Choice

The analysis performed on the Cravens data to this point is good preparation for choos­ing a final model, but a careful analysis of the residuals should be conducted before the final choice. We want the residual plot for the chosen model to resemble approximately a horizontal band. Let us assume the residuals are not a problem and that we want to use the results of the best-subsets procedure to help choose the model.

The best-subsets procedure shows us that models with more than four variables provide only marginal gains in R². The best four-variable model (Poten, AdvExp, Share, and Ac­counts) also happens to be the four-variable model identified with the stepwise regression procedure.

From Figure 16.17, we see that the model with just AdvExp and Accounts is also good with an R² = 77.51%. The simpler two-variable model might be preferred, for instance, if it is difficult to measure market potential (Poten). However, if the data are readily available and highly accurate predictions of sales are needed, the model builder would clearly prefer the model with all four variables.

Source:  Anderson David R., Sweeney Dennis J., Williams Thomas A. (2019), Statistics for Business & Economics, Cengage Learning; 14th edition.