Qualitative and Limited Dependent Variables by using EViews

1. MODELS WITH BINARY DEPENDENT VARIABLES

We will illustrate binary choice models using an important problem from transportation economics. How can we explain an individual’s choice between driving (private transportation) and taking the bus (public transportation) when commuting to work, assuming, for simplicity, that these are the only two alternatives? We represent an individual’s choice by the dummy variable

If we collect a random sample of workers who commute to work, then the outcome y will be unknown to us until the sample is drawn. Thus, y is a random variable. If the probability that an individual drives to work is p, then P[y = 1] = p . It follows that the probability that a person uses public transportation is P[y = 0] = 1 – p. The probability function for such a binary random variable is

where p is the probability that;; takes the value 1. This discrete random variable has expected value E(y) = p and variance var( y) = p(1-p).

What factors might affect the probability that an individual chooses one transportation mode over the other? One factor will certainly be how long it takes to get to work one way or the other. Define the explanatory variable

x – (commuting time by bus – commuting time by car)

There are other factors that affect the decision, but let us focus on this single explanatory variable. A priori we expect that as x increases, and commuting time by bus increases relative to commuting time by car, an individual would be more inclined to drive. That is, we expect a positive relationship between x and p, the probability that an individual will drive to work.

1.1. Examine the data

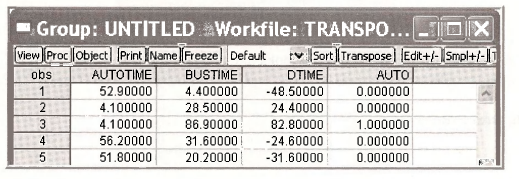
Open the workfile transport.wfl. Save the workfile with an new name to transportchapl6.wfl so that the original workfile will not be changed. Highlight the series AUTOTIME, BUSTIME, DTIME and AUTO in order. Double-click in the blue to open the Group. The data are shown on the next page.

The key point is that AUTO, which is to be the dependent variable in the model, only takes the values 0 and 1.

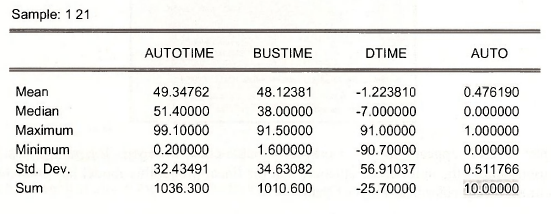
Obtain the descriptive statistics from the spreadsheet view: Select View/Descriptive Stats/Common Sample.

The summary statistics will be useful later, but for now notice that the SUM of the AUTO series is 10, meaning that of the 21 individuals in the sample, 10 take their automobile to work and 11 take public transportation (the bus.)

1.2. The linear probability model

Our objective is to estimate a model explaining why some choose AUTO and some choose BUS transportation. Because the outcome variable is binary, its expected value is the probability of observing AUTO = 1,

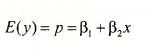
The model

is called the linear probability model. It looks like a regression, but as noted in POE, page 420, there are some problems. Nevertheless, apply least squares using y = A UTO and x = DTIME.

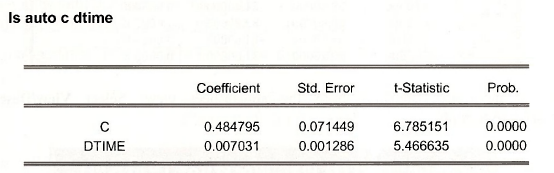
The problems with this estimation procedure can be observed by examining the predicted values, which we call PHAT. In the regression window select the Forecast button

[Forecast]

Fill in the dialog box with a Forecast name.

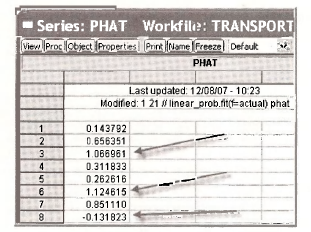
An object PHAT appears in the workfile. Double-click to open. Examining just a few observations shows the unfortunate outcome that the linear probability model has predicted some probabilities to be greater than 1 or less than 0.

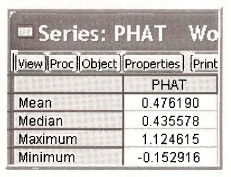
Now, examine the summary statistics for PHAT from the spreadsheet view, by selecting View/Descriptive Statistics & Tests/Stats Table.

Note that the average value of the predicted probability is .476, which is exactly equal to the fraction (10/21) of riders who choose AUTO in the sample. But also note that the minimum and maximum values are outside the feasible range.

1.3. The probit model

The probit statistical model expresses the probability p that v takes the value 1 to be

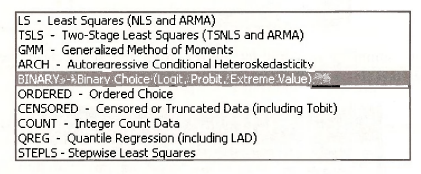
where Φ(z) is the probit function, which is the standard normal cumulative distribution function (CDF). This is a nonlinear model because the parameters β₁ and β₂ are inside the very nonlinear function Φ(•). Using numerical optimization procedures, that are outside the scope of this book, we can obtain maximum likelihood estimates. From the EViews menubar select Quick/Estimate Equation. In the resulting dialog box, click the pull down list in the Method section of Estimation settings

A long list of options appears. Choose BINARY.

The estimation settings should look like

In the Equation specification box enter the equation as usual, but select the radio button for Probit.

Click OK. The estimation results appear on the next page. In most ways the output looks similar to the regression output we have seen many times. The Coefficients, Std. Error and Prob. columns are familiar. There are many items included in the output you will not understand, and we are just omitting. However, we note the following:

• The Method: ML means that the model was estimated by maximum likelihood.
• The usual t-Statistic has been replaced by z-Statistic. The reason for this change is that the standard errors given are only valid in large samples. As we know the t-distribution converges to the standard normal distribution in large samples, so using “z” rather than “t” recognizes this fact. The p-values Prob. are calculated using the N(0,1) distribution rather than the t-distribution.

• In the bottom portion of the output we see an R² value called McFadden R-squared. This is not a typical R” and cannot be interpreted like an R². As a child your mother pointed to a pan of boiling water on the stove and said Hot! Don’t touch! We have a similar attitude about this value. We don’t want you to “get burned,” so please disregard this number until you know much more.
• The LR statistic is comparable to the overall F-test of model significance in regression. It is a test statistic for the null hypothesis that all the model coefficients are zero except the intercept, against the alternative that at least one of the coefficients is not zero. The LR statistic has a chi-square distribution if the null hypothesis is true, with degrees of freedom equal to the number of explanatory variables, here Prob(LR statistic) is the p-value for this test, and it is used in the standard way. If p < a then we reject the null hypothesis at the a level of significance.

1.4. Predicting probabilities

The “prediction” problem in probit is to predict the choice by an individual. We can predict the probability that individuals in the sample choose AUTO. In order to predict the probability that an individual chooses the alternative AUTO (y) = 1 we can use the probability model p = Φ(β₁ + β₂x) using estimates β₁ = -0.0644 and β₂ = 0.02999 of the unknown parameters obtained in the previous section.. Using these we estimate the probability p to be

By comparing to a threshold value, like 0.5, we can predict choice using the rule

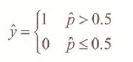
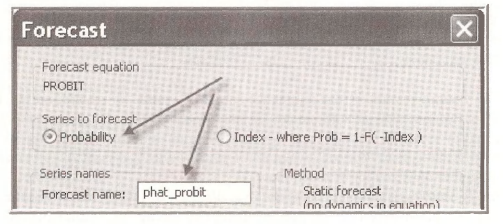
The predicted probabilities are easily obtained in EViews. Within the probit estimation window select Forecast.

In the resulting Forecast dialog box choose the Series to forecast to be the Probability, and assign the Forecast name PHAT PROBIT. Click OK.

Open the series PHAT_PROBIT by double-clicking the series icon in the workfile window. The values of the predicted probabilities are given for each individual in the sample, based on their actual DTI ME.

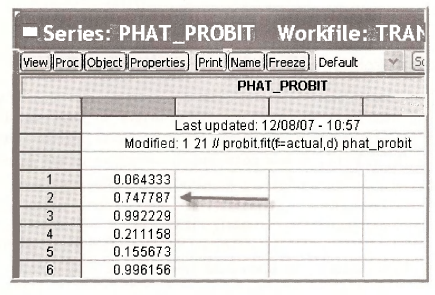
It is useful to see that these predicted probabilities can be computed directly using the EViews function @cnorm which is the CDF of a standard normal random variable, what we have called “Φ”. EViews places the estimates of the unknown parameters in the coefficient vector C,

The predicted probabilities from the two methods are the same

1.5. Marginal effects in the probit model

In this model we can examine the effect of a one unit change in jc on the probability that y = 1 by considering the derivative, which is often called marginal effect by economists.

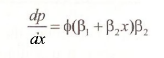
This quantity can be computed using the EViews function @dnorm, which gives the standard normal density function value, that we have represented by Φ. To generate the series of marginal effects for each individual in the sample, enter the command

series mfx_probit = @dnorm(c(1)+c(2)*dtime)*c(2)

The marginal effect at a particular point uses the same calculation for a particular value of DTIME, such as 20.

scalar mfx_probit_20 = @dnorm(c(1)+c(2)*20)*c(2)

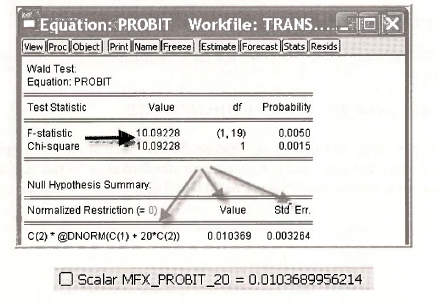
EViews is very powerful, and one of its features is the calculation of complicated nonlinear expressions involving parameters and computed their standard error by the “Delta” method. In the PROBIT estimation w indow, select View/Coefficient Tests/Wald – Coefficient Restrictions.

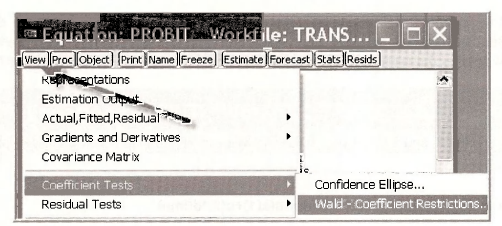
In the dialog window enter the expression for the marginal effect, assuming DTIME = 20, setting it equal to zero as if it were a hypothesis test.

This returns the F-test statistic for the null hypothesis that the marginal effect is zero. Thep-value is 0.005 leading us to reject the null hypothesis that additional BUS time has no effect on the probability of AUTO travel when DTIME = 20. Furthermore, the Value and the Std. Err. are computed. The value matches the scalar MFX PROBIT 20 computed earlier, and we now have a standard error that can be used to construct a confidence interval. Very cool.

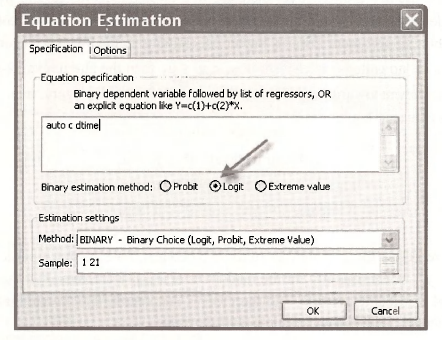
To make the estimations using the Logit model simply change the Equation Estimation entries to

2. ORDERED CHOICE MODELS

In POE Chapter 16.3 we considered the problem of choosing what type of college to attend after graduating from high school as an illustration of a choice among unordered alternatives. However, in this particular case there may in fact be natural ordering. We might rank the possibilities as

The usual linear regression model is not appropriate for such data, because in regression we would treat the y values as having some numerical meaning when they do not. When faced with a ranking problem, we develop a “sentiment” about how we feel concerning the alternative choices, and the higher the sentiment the more likely a higher ranked alternative will be chosen. This sentiment is, of course, unobservable to the econometrician. Unobservable variables that enter decisions are called latent variables, and we will denote our sentiment towards the ranked alternatives by y*, with the “star” reminding us that this variable is unobserved.

As a concrete example, let us think about what factors might lead a high school graduate to choose among the alternatives “no college,” “2-year college” and “4-year college” as described by the ordered choices above. For simplicity, let us focus on the single explanatory variable GRADES. The model is then

This model is not a regression model because the dependent variable is unobservable. Consequently it is sometimes called an index model.

Because there are M = 3 alternatives there are M -1 = 2 thresholds μ₁ and μ₂, with μ₁ < μ₂. The index model does not contain an intercept because it would be exactly collinear with the threshold variables. If sentiment towards higher education is in the lowest category, then y* < μ₁ and the alternative “no college” is chosen, if μ₁ < y* < μ₂ then the alternative “2-year college” is chosen, and if sentiment towards higher education is in the highest category, then y* > μ₂ and “4- year college” is chosen. That is,

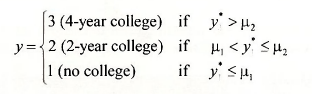
We are able to represent the probabilities of these outcomes if we assume a particular probability distribution for y , or equivalently for the random error e_i. If we assume that the errors have the standard normal distribution, N(0,1), and the CDF is denoted d>. an assumption that defines the ordered probit model, then we can calculate the following:

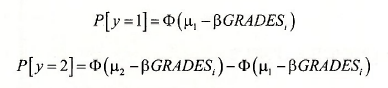
and the probability that y = 3 is

In this model we wish to estimate the parameter p, and the two threshold values pi and p2. These parameters are estimated by maximum likelihood.

In EViews open the workfile nelssmalLwfl. Save it under the name nels small oprobitwfl. The dependent variable of interest is PSECHOICE and the explanatory variable is GRADES. Select Quick/Estimate Equation. In the drop down menu of estimation methods choose Ordered Choice.

Enter the estimation equation with NO INTERCEPT. Make sure the Normal radio button is selected so that the model is Ordered Probit.

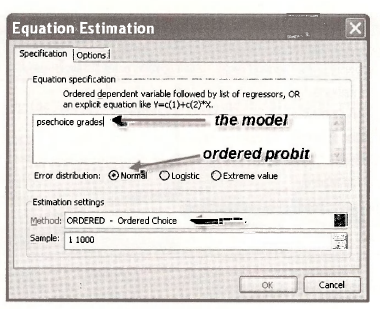
The results, edited to remove things that are not of interest, are

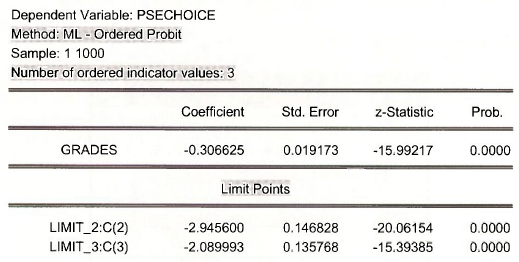
The coefficient of GRADES is the maximum likelihood estimate (3. The values labeled LIMIT_2:C(2) and LIMIT 3:C(3) are the maximum likelihood estimates of p, and p₂. The notation points out that the these parameter estimates are saved into the coefficient vector as C(2) and C(3). C(l) contains J3. Name this equation OPROBIT.

2.1. Ordered probit predictions

To predict the probabilities of various outcomes, as shown on page 436 of POE, we can again use the computing abilities of EViews. In the OPROBIT estimation window select View/Coefficient Tests/Wald – Coefficient Restrictions.

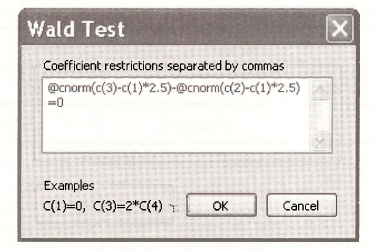
To compute the probability that a student with GRADES = 2.5 will attend a 2-year college we calculate

Enter into the Wald Test dialog box

The predicted probability is the relatively low 0.078, which makes sense because GRADES =2.5 is very high on the 13 points scale..

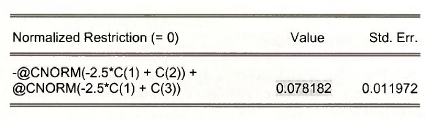
We can use the same general approach to compute the probabilities for each option for all the individuals in the sample. Recall that the maximum likelihood estimates of μ₁ and μ₂ are saved into the coefficient vector as C(2) and C(3). C(1) contains β.

Open a Group showing the GRADES, PSECHOICE and the predicted probabilities.

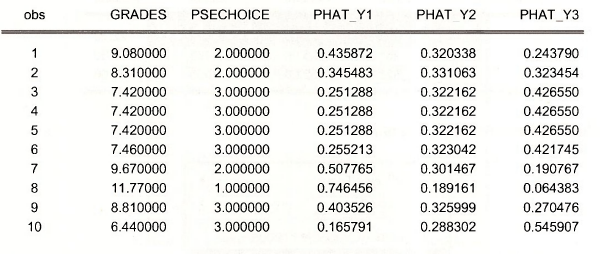
A standard procedure is to predict the actual choice using the highest probability. Thus we would predict that person 1 would attend no college, and the same with person 2. Both of these predictions are in fact incorrect because they choose a 2-year college. Individual 3 we predict will attend a 4-year college, and they did.

In the EViews window containing the estimated model OPROBIT, select View/Dependent Variable Frequencies

We see the choices made in the data

Now select View/Prediction Evaluation.

Using the “highest probability” prediction rule, EViews calculates

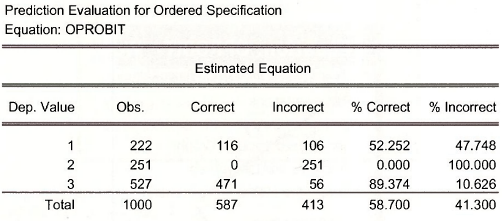
This model, being a very simple one, has a difficult time predicting who will attend 2-year colleges, being incorrect 100% of the time.

2.2. Ordered probit marginal effects

The marginal effects in the ordered probit model measure the changed in probability of choosing a particular category given a 1-unit change in an explanatory variable. The calculations are different by category. The calculations involve the standard normal probability density function, denoted Φ and calculated in EViews by @dnorm. For example the marginal effect of GRADES on the probability that a student attends no college is

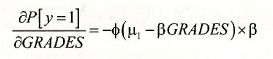
In the OPROBIT window select View/Coefficient Tests/Wald – Coefficient Restrictions. In the dialog box enter

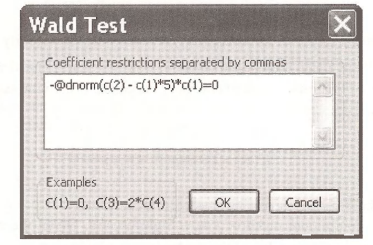
Recalling that a higher value of GRADES is a poorer academic performance, we see that the probability of attending no college increases by 0.045 for a student with GRADES = 5.

The marginal effect calculation can be carried out for each person in the sample using the command

series mfx_y1 = – @dnorm(c(2) – c(1)*grades)*c(1)

Open a Group showing GRADES and this marginal effect. Note that increasing GRADES by 1- point (worse grades) increases the probabilities of attending no college, but for students with better grades (GRADES lower) the effect is smaller.

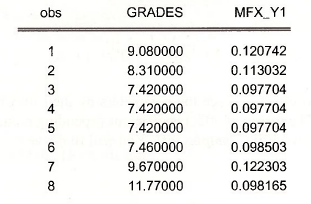
3. MODELS FOR COUNT DATA

If Y is a Poisson random variable, then its probability function is

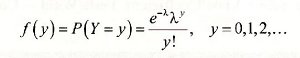
The factorial (!) term y! = y x (y-1)x(y-2) x…x 1. This probability function has one parameter, λ, which is the mean (and variance) of Y. In a regression model we try to explain the behavior of E(y) as a function of some explanatory variables. We do the same here, keeping the value of E(y)>0 by defining

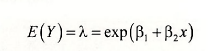
This choice defines the Poisson regression model for count data.

Prediction of the conditional mean of y is straightforward. Given the maximum likelihood estimates β₁ and β₂, and given a value of the explanatory variable x₀, then

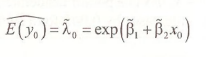
This value is an estimate of the expected number of occurrences observed, if x takes the value x₀. The probability of a particular number of occurrences can be estimated by inserting the estimated conditional mean into the probability function, as

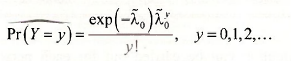
The marginal effect of a change in a continuous variable x in the Poisson regression model is not simply given by the parameter, because the conditional mean model is a nonlinear function of the parameters. Using our specification that the conditional mean is given by

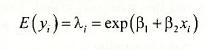
and using rules for derivatives of exponential functions, we obtain the marginal effect

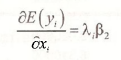
To estimate this marginal effect, replace the parameters by their maximum likelihood estimates, and select a value forx. The marginal effect is different depending on the value ofx chosen.

To illustrate open the workfile olympics.wfl. You will find a very rude message.

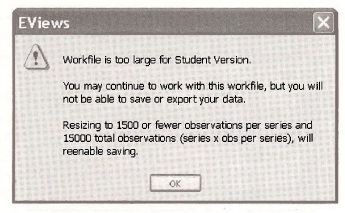
This workfile is too large because there are too many observations. The definition file Olympics.def shows that there are 1610 observations.

We can still operate with the workfile, but we cannot save it even if we delete some variables. Give this a try, deleting the variables that are needed in this example.

The example in the book uses only data from 1988. To modify the sample, click the Sample button on the EViews main menu.

In the Sample dialog box add the IF condition

The workfile window now shows that the estimation sample is 179 observations from the year 1988.

Despite these changes the file still cannot be saved with the Student Version of EViews 6. Your options are to switch to the full version, or to make sure you print out all intermediate results as you go along.

3.1. Examine the data

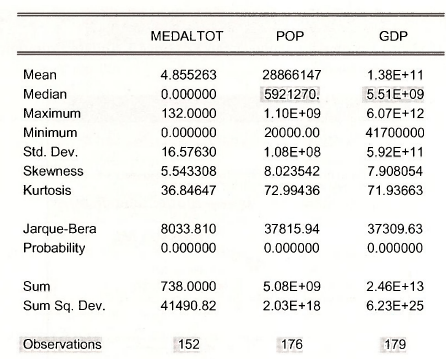
Open a group consisting of MEDALTOT, POP and GDP. Obtain summary statistics for the individual samples

Finding the summary statistics for individual samples is important when some observations are missing, or NA.

Note that there are 152 observations for MEDALTOT, 176 for POP and 179 for GDP.

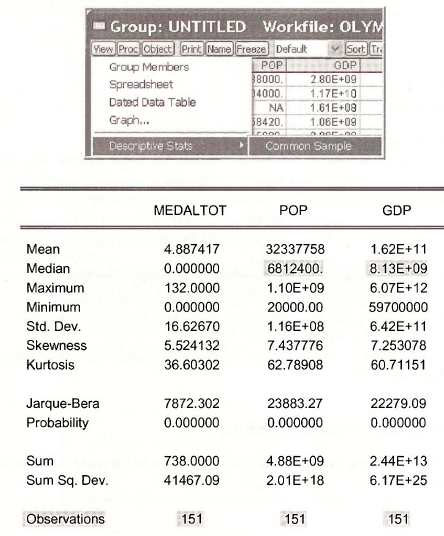
Obtaining summary statistics for the Common Sample we find that 151 observations are available on all 3 variables.

3.2. Estimating a Poisson model

To estimate the model by maximum likelihood choose Quick/Estimate Equation. In the dialog box make the choices shown below.

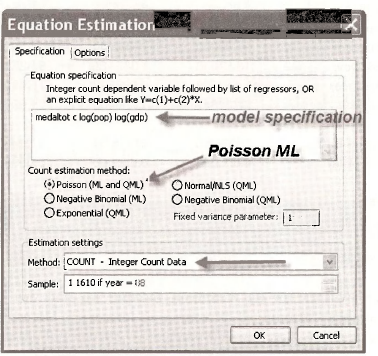
The estimated model is

Note that the number of observations used in the estimation is only 151, which is the number of observations common to all variables.

Despite the fact that the workfile cannot be saved, we save these estimation results as an object named POISSON REG.

3.3. Prediciting with a Poisson model

In the estimation window click Forecast. Choose the Series to forecast as Expected dependent var. and assign a name

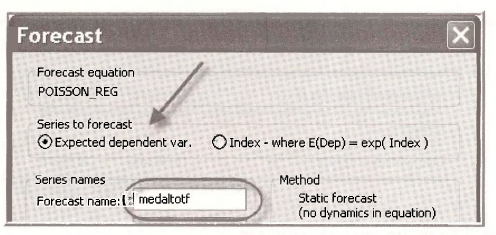
Recall that the expected value of the dependent variable, in a simple model, is given by

The forecast can be replicated using the following command

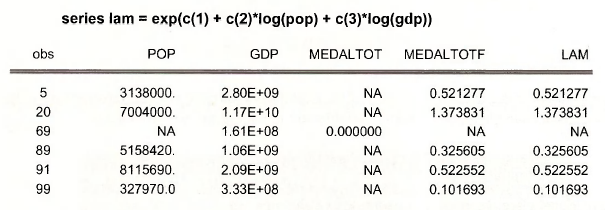
We have shown a few values.

To compute the predicted mean for specific values of the explanatory variables we again use the trick of applying the “Wald test.” Select View/Coefficient TestsAVald – Coefficient Restrictions. We must choose some values for POP and GDP at which to evaluate the prediction. Enter the median values from the individual samples for POP and GDP.

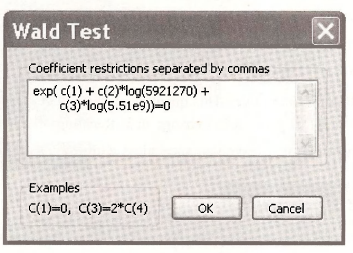
The result shows that for these population and GDP values we predict that 0.8634 medals will be won.

3.4. Poisson model marginal effects

As shown in POE equation (16.29) the marginal effects in the simple shown in the simple Poisson model

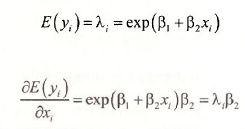
This marginal effect is correct if the values of the explanatory variable x is not transformed. In the Olympics medal example the explanatory variables are in logarithms, so the model is

and the marginal effect is, using the chain rule of differentiation,

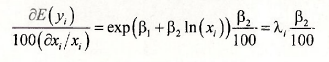
While this does not necessarily look very pretty, it has a rather nice interpretation. Rearrange it as

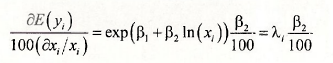
Are you still not finding this attractive? This quantity can be called a semi-elasticity, because it expresses the change in E(y) given a 1% change in x. Recalling that E(y_i ) = λ_i we can make one further enhancement that will leave you speechless with joy. Divide both sides by E(y) to obtain

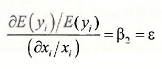
The parameter β₂ is the elasticity of the output y with respect to x. A 1 % change in x is estimated to change E[y) by β₂%.

In the Olympics example, based on the estimation results, we conclude that a 1% increase population increases the expected medal count by 0.18%, and a 1% in GDP increases expected medal count by 0.5766%.

4. LIMITED DEPENDENT VARIABLES

The idea of censored data is well illustrated by the Mroz data on labor force participation of married women. Open the workfile mroZ’Wfl. You will receive an unpleasant warning when using the Student Version of EViews 6:

However, this problem can be fixed by deleting some variables. Delete the variables indicated below.

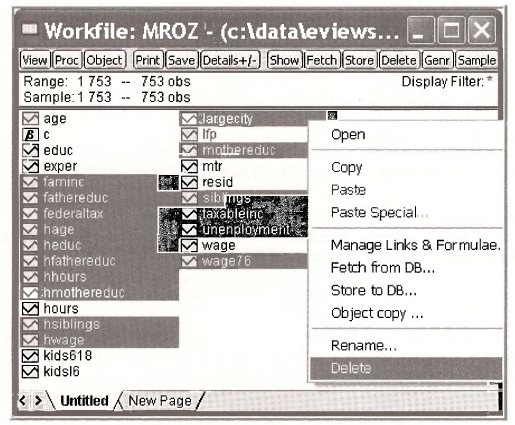
EViews now tells us we are OK, can save the workfile

Save the workfile as mrozjtobitwfl to as to keep the original file intact.

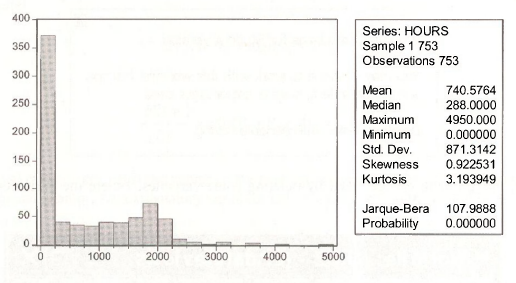
A Histogram of the variable HOURS shows the problem with the full sample. There are 753 observations on the wages of married women but 325 of these women did not engage in market work, and thus their HOURS = 0, leaving 428 observations with positive HOURS.

4.1. Least squares estimation

We are interested in the equation

The question is “How shall we treat the observations with HOURS = 0”?

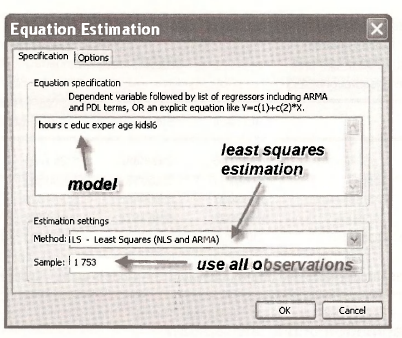
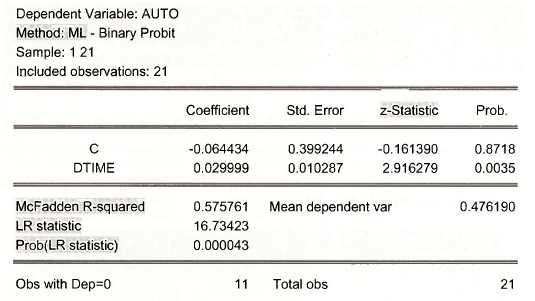
A first solution is to apply least squares to all the observations. Select Quick/Estimate Equation and fill in the Equation Estimation dialog box as follows:

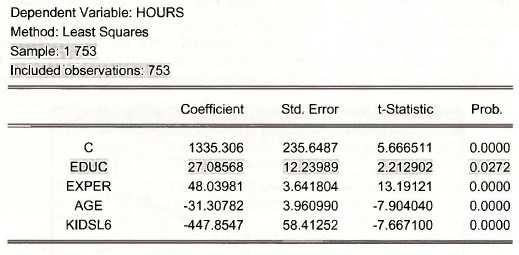
The estimation results are

Repeat the estimation using only those women who “participated in the labor force.” Those women who worked are indicated by a dummy variable LFP which is 1 for working women, but zero otherwise.

The estimation results are shown below. Note that the included observations are 428. The estimation results now show the effect of education (EDUC) to have a negative, but insignificant, affect on HOURS. In the estimation using all the observations EDUC had a positive and significant effect on HOURS.

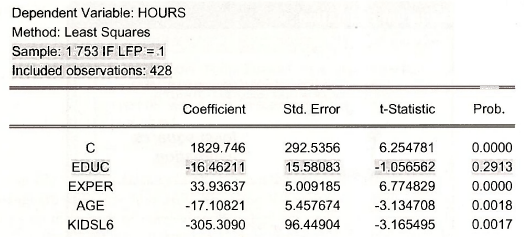
The least squares estimator is biased and inconsistent for models using censored data.

4.2. Tobit estimation and interpretation

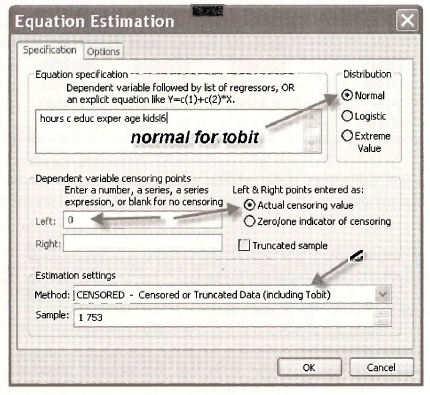
An appropriate estimation procedure is Tobit, which uses maximum likelihood principles. Select Quick/Estimate Equation. In the Equation Estimation window fill in the options as shown below. Tobit estimation is predicated upon the regression errors being Normal, so tick that radio button. In our cases the observations that are “censored” take the actual value 0, and the dependent variable is said to be Left censored because 0 is a minimum value and all relevant values of HOURS are positive. The Estimation settings show the method to include Tobit.

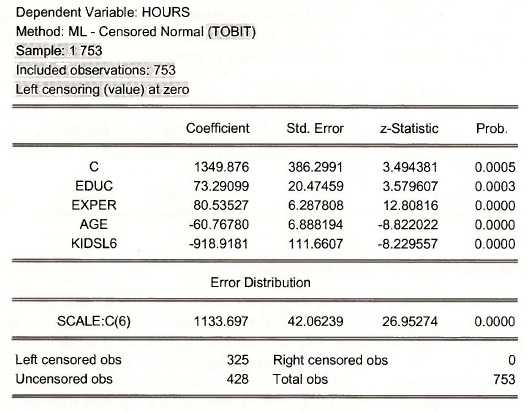
The estimation output shows the usual Coefficient and Std. Error columns. Instead of a t- Statistic EViews reports a z-Statistic because the standard errors are only valid in large samples, making the test statistic only valid in large samples, and in large samples a t-statistic converges to the standard normal distribution. The p-value Prob. is based on the standard normal distribution.

The parameter called SCALE:C(6) is the estimate of σ, the square root of the error variance. This value is an important ingredient in Tobit model interpretation. As noted in POE, equation (16.35), the marginal effect of an explanatory variable in a simple model, is

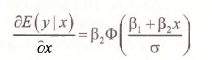
where as usual Φ is the CDF of a standard normal variable. To evaluate the marginal effect of EDUC on HOURS, given that HOURS > 0, we can use Wald test dialog box. Select View/Coefficient Tests/Wald – Coefficient Restrictions. Enter in the expression for the marginal effect of EDUC at the sample means, as shown on page 447 of POE.

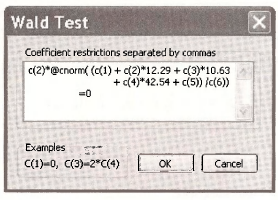
The obtained value is slightly different than the value in the text. Slight differences in results are inevitable when carrying out complicated nonlinear estimations and calculations. The maximum likelihood routines are all slightly different, and stop when “convergence” is achieved. These stopping rules are different from one software package to another.

4.3. The Heckit selection bias model

If you consult an econometrician concerning an estimation problem, the first question you will usually hear is, “How were the data obtained?” If the data are obtained by random sampling, then classic regression methods, such as least squares, work well. However, if the data are obtained by a sampling procedure that is not random, then standard procedures do not work well. Economists regularly face such data problems. A famous illustration comes from labor economics. If we wish to study the determinants of the wages of married women we face a sample selection problem. If we collect data on married women, and ask them what wage rate they earn, many will respond that the question is not relevant since they are homemakers. We only observe data on market wages when the woman chooses to enter the workforce. One strategy is to ignore the women who are homemakers, omit them from the sample, then use least squares to estimate a wage equation for those who work. This strategy fails, the reason for the failure being that our sample is not a random sample. The data we observe are “selected” by a systematic process for which we do not account.

A solution to this problem is a technique called Heckit, named after its developer, Nobel Prize winning econometrician James Heckman. This simple procedure uses two estimation steps. In the context of the problem of estimating the wage equation for married women, a probit model is first estimated explaining why a woman is in the labor force or not. In the second stage, a least squares regression is estimated relating the wage of a working woman to education, experience, etc., and a variable called the “Inverse Mills Ratio,” or IMR. The IMR is created from the first step probit estimation, and accounts for the fact that the observed sample of working women is not random.

The econometric model describing the situation is composed of two equations. The first, is the selection equation that determines whether the variable of interest is observed. The sample consists of N observations, however the variable of interest is observed only for n < N of these. The selection equation is expressed in terms of a latent variable z* which depends on one or more explanatory variables w,., and is given by

For simplicity we will include only one explanatory variable in the selection equation. The latent variable is not observed, but we do observe the binary variable

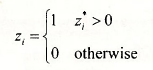
The second equation is the linear model of interest. It is

A selectivity problem arises when y_t is observed only when Z; = 1, and if the errors of the two equations are correlated. In such a situation the usual least squares estimators of J3, and (3₂ are biased and inconsistent.

Consistent estimators are based on the conditional regression function

where the additional variable λ_i is “Inverse Mills Ratio.” It is equal to

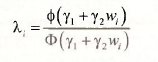
where, as usual, Φ(.) denotes the standard normal probability density function, and Φ(.) denotes the cumulative distribution function for a standard normal random variable. While the value of a is not known, the parameters y₁ and y₂ can be estimated using a probit model, based on the observed binary outcome z_i Then the estimated IMR,

First, let us estimate a simple wage equation, explaining \n{WAGE) as a function of the woman’s education, EDUC, and years of market work experience (EXPER), using the 428 women who have positive wages. Select Quick/Estimate Equation. Fill the dialog box as

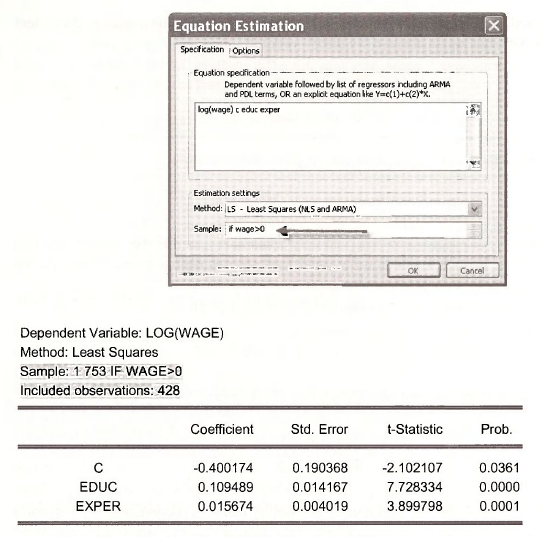
Heckit estimation begins with a probit model estimation of the “participation equation,” in which LFP is taken to be a function of AGE, EDUC, a dummy variable for whether or not the woman as children (KIDS) and her marginal tax rate MTR. Create the dummy variable KIDS using

series kids = (kidsl6 + kids618 > 0)

Select Quick/Estimate equation and fill in the dialog box as shown.

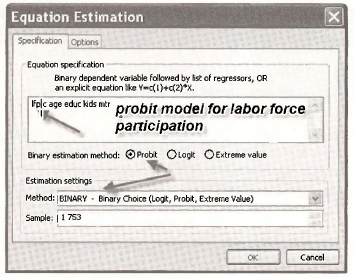
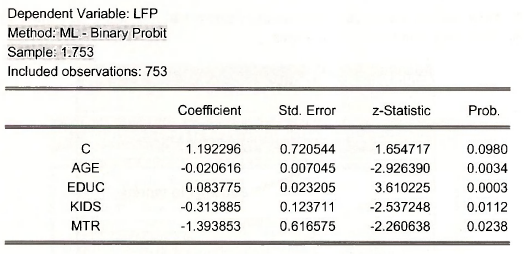
Using all the sample data we obtain

In the Forecast dialog box choose the radio button for Index and give this variable a name.

The inverse Mills ratio is then calculated using the EViews functions for the standard normal pdf @dnorm and the standard normal CDF @cnorm.

series imr = @dnorm(lfpf)/@cnorm(lfpf)

Include the IMR into the wage equation as an explanatory variable, using only those women who were in the labor force and had positive wages.

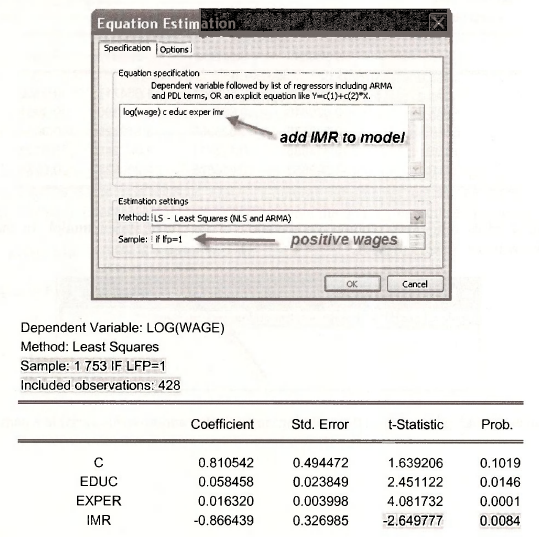
This two-step estimation process is a consistent estimator, however the standard errors Std. Error do not account for the fact the IMR is in fact estimated. If the errors are homoskedastic, we however can carry out a test of the significance of the IMR variable based on the /-statistic that is reported by EViews. This is because under the null hypothesis that there is no selection bias the coefficient of IMR is zero, and thus under the null hypothesis the usual t-test is valid. Here we reject the null hypothesis of no selection bias and conclude that using the two-step Heckit estimation process is needed.

The resulting t-statistic is still significant at the .05 level.

Correct standard errors for the two step estimation procedure are difficult to obtain without specially designed software. Such options, and maximum likelihood estimation of the Heckit model, are available in Limdep and Stata software packages.

Source: Griffiths William E., Hill R. Carter, Lim Mark Andrew (2008), Using EViews for Principles of Econometrics, John Wiley & Sons; 3rd Edition.